"Die Figuren von Fohy - vielleicht das älteste Denkmal der Wissenschaft der Welt"
(G.W. Leibniz)
Erfand George Boole die Binärrechnung, oder haben wir deren Erfinder vergessen?
von Gerd Heinz
Hat die Menschheit bereits den unglaublichen Wohlstand vergessen, den sie durch Mikroprozessoren, Computer, Industrieautomation, Internet und industrialisierte Landwirtschaft erreicht hat? Immerhin führte dieser zu einer Bevölkerungsexplosion, die es vorher nie gab, siehe dazu auch Kap.8 aus "2011 Klima und Kohlekraft". Immer mehr Menschen können ernährt werden. Immer weniger Ingenieure und Techniker sorgen für immer mehr voll- oder teilautomatisierte Produktion auf allen Gebieten und ernähren damit immer mehr Menschen, die sich außerhalb des produktiven Prozesses befinden.
Viele dieser Errungenschaften verdanken wir unserer digitalen oder binären Welt, die von Gottfried Wilhelm Leibniz im Jahre 1701 geprägt wurde.
Aber die daraus entstehenden sozialen Probleme sind nicht vernachlässigbar: Immer weniger Menschen sind mit der Produktion materieller Dinge beschäftigt. Das Potential nichtproduktiver Wähler vergrößert sich von Jahr zu Jahr. Immer mehr Parteien liebäugeln mit der Wählerschaft aus diesem nichtproduktiven Bereich. Einer Wählerschaft, die nicht weiß, das der Strom nicht aus der Steckdose kommt, kann man die Abschaltung aller Atomkraft als Errungenschaft preisen. Kommen solche Parteien an die Macht, resultieren daraus Milliardensubventionen in Technologien, die wenig oder keine marktwirtschaftliche Relevanz haben, die untergehen, sobald die Subventionen verschwinden. Und genau diese Milliarden fehlen dann bei der Erneuerung von Straßen, Brücken oder Gleisen.
Jeder Computer und jedes Handy nutzt sie, jeder Taschenrechner und jede Excel-Tabelle rechnet intern damit, jede Email, jedes Video und jeder Sound besteht aus binären Daten. Auf Festplatten, auf DVDs und in SD-Cards werden sie gespeichert. Über USB- und durch das Ethernet flitzen sie, jeder Bildschirm wird damit angesteuert. In unserer digitalen Welt gibt es nicht viel anderes, auch wenn selbst Programmierer (wenn überhaupt) nur äußerst selten mit Binärwerten zu tun haben.
Wenn wir auf dem PC zwei Dezimalzahlen addieren, dann werden diese im ersten Schritt meist in Binärzahlen konvertiert. Damit wird gerechnet. Dann wird das Ergebnis zurück in Dezimalziffern gewandelt und angezeigt.
Wir alle sollten diese Binärzahlen kennen, oft auch als Dualzahlen bezeichnet. Unsere digitale Welt besteht aus diesen Zahlen. Man denke an binary digit: abgekürzt Bit, oder an Byte (8 Bit), Kilobyte (103 Byte), Megabyte (106 Byte), Gigabyte (109 Byte) oder Terabyte (1012 Byte). Den Begriff der Binärzahlen führte der letzte Universalgelehrte ein. Es war Gottfried Wilhelm Leibniz, der nicht nur die Binärzahlen und die Rechnung mit ihnen erfand, sondern dem wir auch die Differential- und Integralrechnung heutige Art verdanken.
Pro Stelle stehen nur die Werte 0 und 1 zur Verfügung. Dafür gibt es viele Stellen: Der erste frei am Markt gehandelte Mikrocontroller, der Intel i4004 hatte 1971 gerade einmal vier Binärstellen, genannt 4 Bit. Damit konnte genau eine Hexadezimalziffer (0...15 oder 0...F) verarbeitet werden. In einem Schritt konnten damit zwei (Hexa- oder Dezimal-) Ziffern bearbeitet werden. Dann folgten Mikrocontroller mit 8 Bit, 16 Bit und 32 Bit. Heute haben wir meist 64 Bit Controller in unseren Smartphones oder PCs.
Diese können 264 oder 18·1018 Werte parallel verarbeiten. In einem 64 Bit Wert können wir jede natürliche Zahl bis zu ebendieser Größe speichern. Und der erste Mikrocontroller hatte deshalb vier Bit, weil sich damit genau eine Dezimalziffer (oder auch eine Hexadezimalziffer) darstellen ließ, 24 = 16. Das sind die Ziffern 0...9, a, b, c, d, e, f.
Größere natürliche Zahlen lassen sich mit einer einfachen Bildungsregel beschreiben. Dazu summieren wir die Stellen entsprechend der Zweierpotenz. So ist die Zahl
Die Rechenregeln, so meint man in der deutschsprachige Wikipedia, stammen vom englisch/irischen Mathematiker, Logiker und Philosoph Georg Boole (1815 bis 1864). Der allgemein in Programmiersprachen und Compilern verwendete Datentyp für binäre Zahldarstellungen ist - wen wundert es - der Typ "boolean".
Jeder, der schon einmal eine digitale Schaltung mit NAND, NOR, XOR, Halbaddern, Volladdern, Registern oder Flipflops aufgebaut hat, der kennt die sogenannte "Boolesche Algebra".
Nun wissen wir aus anderen Bereichen von Wissenschaft und Technik, daß nicht immer der Erfinder geehrt wird, sondern oft auch Plagiateure. Oder Personen, die sich um die Verbreitung einer Erkenntnis verdient machten. Oder Menschen, die ein Gespür für die Vermarktung von Wissen hatten.
Über ein Jahrhundert vor Georg Boole lebte Gottfried Wilhelm Leibniz (1646 bis 1716). Er formulierte die noch heute üblichen Schreibweisen der Infinitesimalrechnung und Differentialrechnung, trug zur Algebra (Leibnitz-Matrix) bei, baute die ersten Rechenmaschinen mit Staffelwalzen und erste Chiffriermaschinen. Und er korrespondierte in sechs Sprachen. Er galt als der letzte Universalgelehrte.
Da ich mein Leben lang immer wieder auch digitale Schaltungen entwickelt habe, erschrak ich um die Jahrtausendwende herum über eine Seite eines Vortrages, die Leibniz vor der französischen Akademie 1701 gehalten haben soll.
Ich entdeckte diese Seite damals wohl eher zufällig irgendwo im Internet. Leider ist sie bis 2023 weder in der englischsprachigen [2] , noch in der deutschsprachigen [1] Wikipedia zu finden. Dafür findet Google sie in zig anderssprachigen Wikis unter diesem Link [5].
Mich verblüffte die Genialität der Notation, die mir als Praktiker so geläufig war, als wären mir diese Zeilen gerade gestern von einem Kollegen überreicht worden. Und mich verblüffte die einzigartige Eleganz und Kompaktheit der Darstellung. Wofür wir als Studenten ein Semester lang Vorlesungen hatten, das drückt er auf einer Seite aus (Memoires de l'Academie Royale, 1703, Seite 86):
Abb.1: Korrigierte Seite 86 aus dem Vortrag vor der französischen Akademie. Am linken Rand führt Leibniz die Binärzahlen ein, um dann in der Mitte sogleich Beispiele für Addition, Subtraktion, Multiplikation und Division anzugeben. Zwei Beispiele für die Addition von Binärzahlen sind in der rechten, oberen Ecke zu erkennen.
Beim Versuch, die Beispiele nachzurechnen, fiel mir auf, daß ich es seit dem Aufkommen der Taschenrechner gegen Ende der 1970er Jahre verlernt hatte, schriftlich zu multiplizieren und zu dividieren: Vielleicht versuchen auch Sie einmal, ihre Kenntnisse aufzufrischen und die Beispiele nachzurechnen?
Wir wollen versuchen, Leibniz' Rechnungen zu verstehen.
Bei der Addition scheint es keinerlei Interpretationsspielraum zu geben, 0+0=0; 1+0=1; 0+1=1; 1+1=0 ü=1; den Übertrag ü addiert er in gewohnter Weise auf die nächste Stelle, er merkt sich den Übertrag mit einem kleinen Punkt.
Bei der Subtraktion sind Interpretationen möglich. Von allen modernen Computern wissen wir, daß sie das
Zweierkomplement nutzen, um eine Subtraktion auf eine Addition zurückzuführen. Dabei wird die zu subtrahierende Ziffer negiert, dann wird eins addiert.
Alle beteiligten Zahlen nutzen dabei die erste Ziffer (MSB) nicht, sie stellt das Vorzeichen dar.
Diese großartige Idee hatte Leibniz offenbar noch nicht, sie wurde erst von Konrad Zuse mit seiner
Zuse-Z3
Rechenmaschine am 12. Mai 1941 der Öffentlichkeit vorgestellt.
Betrachtet man die Rechnung von Leibniz, so subtrahiert er nach folgender Regel: 1-0=1; 1-1=0; 0-0=0; 0-1=1 ü=-1; er rechnet mit einem negativen Übertrag. Mit Zuses Zweierkomplement geht das einfacher. Aus der Subtraktion entsteht dabei eine Addition ohne negativen Übertrag.
Multiplikation: Die Schreibweise ist nicht ganz die, die meiner Generation beigebracht wurde, dennoch liegen die Dinge klar auf der Hand, er multipliziert Stelle für Stelle und addiert die um die Stelle verschobenen Teile wie gewohnt. Wie bei der Addition notiert er den Übertrag mit einem Punkt.
Die Division ist schwer nachvollziehbar. Entweder hatte Leibniz einen speziellen Stil, oder es haben sich auch hier Druckfehler eingeschlichen. Man beachte die Einsen, die wie X aussehen: Es sind durchgestrichene Einsen, deren Verwendung sich dem Autor nicht erschließt. Deshalb hier nur Ansätze, die man für die Aufgabe 15/3 = 5 erwarten würde:
1111 / 11 = 101 11 denn 1 · 11 = 11 ——— 01 0 denn 0 · 11 = 00 ——— 11 11 denn 1 · 11 = 11 ——— 000
In verkürzter Notation:
1111 / 11 = 101 11 00 (00 entfällt) 11 ———— 0
Weil die Null-Produkte nicht beachtet werden müssen, könnte man in Kurzform auch schreiben:
1111 / 11 = 101 11 11 ———— 0Verwendet man die Leibnizsche Schreibweise, könnte man noch einfacher schreiben:
1111 ∥ 15 11 ∥ 3 ———— ∥ —— 0101 ∥ 5
Der Rechengang dahinter wäre: 1 geteilt durch 11 ist 0 - hinschreiben. Dann 11 geteilt durch 11 ist 1 - hinschreiben. Dann 1 geteilt durch 11 ist 0 - hinschreiben. Zuletzt 11 geteilt durch 11 ist 1 - hinschreiben.
Vergleicht man die Rechnung mit dem Original, so wäre wahrscheinlich, daß Leibniz die Zwischensummen direkt in der zweiten Reihe antrug. Allerdings ist seine 11 in der letzten Zeile unklar. Es kann sich nur um die 3 handeln, die in der ersten Zeile fehlt. Wahrscheinlich hat hier der Schriftsetzer nicht aufgepaßt.
Als Hard- und Softwareentwickler war mir nach dem Studium dieser Seite klar, daß Leibniz schon damals erste, binär arbeitende Rechner hätte bauen können, hätte er die dazu nötigen Schaltkreise gehabt.
George Booles Darstellungen erscheinen mir dagegen vergleichsweise umständlich theoretisch überzogen. Das verrät ein Blick in sein 150 Jahre später (1848) erschienenes Hauptwerk "The Calculus of Logic" [3], siehe auch [12]. In der Tat ist in seinem Hauptwerk keinerlei Bezug auf Leibniz zu finden.
Es ist zwar ein toller Titel, aber die Leibnizschen Erkenntnisse zur binären Zahldarstellung und zur binären Arithmetik fehlen leider vollständig. Leibniz wird nicht einmal erwähnt. Stellt sich die Frage, ob Boole schon die Leibnizschen Binärzahlen in der Form der "Table des Nombres" kannte.
Und noch schlimmer: Boole erwähnt noch nicht einmal die Möglichkeit, mit Binärzahlen zu rechnen: Zu addieren, zu substrahieren, zu multiplizieren und zu dividieren! Sein Werk gilt ausschließlich der logischen Verknüpfung von Variablen.
Warum ist das zu erwähnen? Noch heute ist Philosophen, die sich mit Logik befassen, offenbar nicht klar, daß Logikbausteine als TTL-Gatter oder als Logikgatter in integrierten Schaltkreisen die Grundlage der Mikroelektronik, das Fundament der Informatik, Rechentechnik, Kommunikationstechnik und Automatisierungstechnik - kurz die Grundlage unserer Industrie und unseres Wohlstands - bilden.
Auch ist meist nicht klar, daß ausnahmslos alle unsere Computertechnik - vom PC bis zum Handy - mit Logikgattern funktioniert, aus denen die Addierwerke und Multiplizierer von Leibniz/Zuse aufgebaut sind.
Noch immer wird philosophische Logik auf sehr merkwürdige Weise von Leibnizscher Algebra mit Binärzahlen separiert. Man unterscheidet zwischen mathematischer Logik und anderen Arten.
Für den Studenten ist oft überhaupt nicht erkennbar, daß Boolsche Logik und Leibnizsche Algebra das Fundament sind, auf dem sich tausende Schnörkel bildeten.
So ist es an der Zeit, anzuerkennen, daß es Techniker waren, die die vielen nebulösen Logiken auf den Punkt brachten: Auf eine widerspruchsfreie, technische Basis, die machbar ist und die in Milliarden von Geräten weltweit widerspruchsfrei funktioniert.
Um z.B. die logischen Grundfunktionen AND, OR und XOR zu verstehen, hat man sich nur ein paar Eselsbrücken zu merken. AND: eine Null an einem Eingang siegt; OR: eine Eins an einem Eingang siegt; XOR: alle Null oder alle Eins siegen. Siegen heißt, der Ausgang geht auf Eins. Schlußendlich wird noch eine Negation NEG gebraucht: aus 1 wird 0 und aus 0 wird 1.
Sicher muß man auch eine Logikschaltung minimieren können. Aber dafür ist die wiederum hundert Jahre später erfundene Karnough-Tafel [10] besser geeignet.
Um zu verstehen, wie Computer heute addieren, schaue man sich einen Volladder an. Dieser besitzt einen zusätzlichen Eingang für den hereinkommenden Übertrag cin und einen zusätzlichen Ausgang für den hinausgehenden Übertrag cout. Die Leitungen x und y sind die Summanden, s ist die Summe der jeweils zu berechnenden Stelle.
Übersetzen wir Algebra volkstümlich mit "Rechnen", dann ist der Begriff "Boolesche Algebra" schlicht und ergreifend falsch. Eine "Boolesche Algebra" hat nie existiert, dafür aber existieren sehr real
die "Boolesche Logik" die "Leibniz-Algebra" mit Binärzahlen und "Zuses Zweierkomplement"- Darstellung von Binärzahlen.
In der englischen Wikipedia wird Gottfried Wilhelm Leibniz als der "Erfinder der Computer-Wissenschaft" bezeichnet. Zu recht, wie wir hier ganz klar erkennen können. Und die "Boolsche Logik" war Leibniz vielleicht zu trivial, um damit die Kollegen Akademiker zu langweilen? Es wäre zu vermuten.
Für mich stellte sich eine weitere Frage: Wer binär Addieren, Subtrahieren, Multiplizieren und Dividieren kann, der würde vielleicht auch die Grundregeln für die Realisierung eines Volladders mit AND, OR, XOR und NEG (Negation) entwickelt haben können (also die Boolesche Logik)?
Um dafür Hinweise zu finden, suchte ich nach dem Original der Leibnizschen Schrift. Es ist im Jahrgang 1703 der französischen Akademie der Wissenschaften zu Paris zu finden. Der Band wurde allerdings erst im Jahr 1705 abgedruckt [7], siehe das Titelblatt. Leibniz Binärsystem finden wir gut versteckt ab Seite 255, statt wie erwartet von S.85 bis S.89. Aber dank der Hilfe von Dr. Sven Erdner von der Gottfried- Wilhelm- Leibniz- Gesellschaft [8] war es möglich, den Beitrag von Leibniz zu entdecken.
So konnte das Leibniz-Original aus dem Alt- Französischen [6] übersetzt werden; hier ist meine Übersetzung ins Deutsche [9] zu finden. Vielen Dank an den Helfer Rolf Tammer sowie an Googles Übersetzer [13].
Ich bitte um Verständnis, daß die Übersetzung sehr eng am Original vorgenommen wurde. Mir kam es nicht auf sprachliche Eleganz, sondern mehr auf inhaltliche Richtigkeit an.
Leider beschäftigte sich Leibniz im Detail nicht ausführlicher mit Fragen der Logik auf binären Zahlen und der Durchführung der Grundrechenarten Rechenoperationen (plus, minus, mal, durch) mit Binärzahlen.
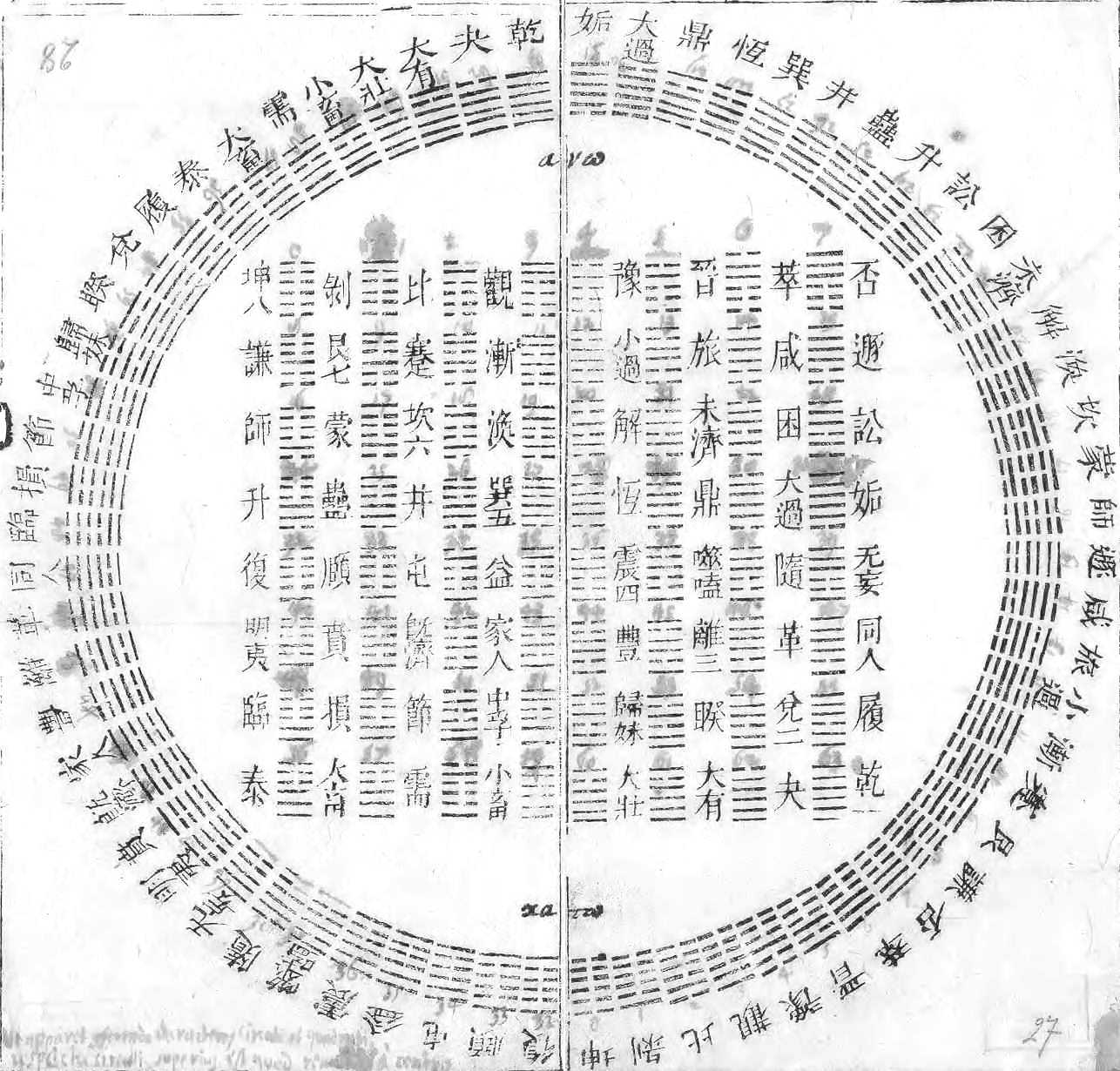Er geht stattdessen auf die "vermutlich 4000 Jahre alten
Linien von Fohy" ein, die von ihm als Binärsystem entschlüsselt werden konnten
[11]. Sie sind heutzutage im Internet als "Ching- oder Yijing- Hexagram" zu finden (Bild rechts) und haben trotz der Leibnizschen Entdeckung des dahinter stehenden Binärsystems nichts von ihrer rein spekulativen, astrologischen und mystischen Bedeutung verloren. Zur mystischen Bedeutung siehe auch die konfuzianischen Bezüge im "Buch der Wandlungen - Yijing" [14], [15].
Bedauerlich, daß ausgerechnet die Leibnizsche Binärrechnung bis heute (2023) unter seinem Namen unbekannt ist.
PS zu Druckfehlern
Das Original [6] enthält auf Seite 86 einen Druckfehler, den ich korrigiert habe: In der zweiten Rechentabelle rechts oben auf Seite 86 muß es heißen 1101 = 13 statt 0101 = 13.
Eine andere Kopie dieser Seite, die in der Wikipedia als *.png verwendet wird [5], hat noch einen zweiten Druckfehler in ebendieser Tabelle, dort fehlt auch noch eine vier, statt 8+1 = 13 muß es heißen 8+4+1 = 13.
Wenn Sie Lehrer sind, dann sollten Sie besser die vom Autor
korrigierte Seite ohne offensichtliche Druckfehler benutzen. Allerdings ist auch diese nicht perfekt.
Die Zeilen zur Division wurden nicht korrigiert, da der Rechenstil für den Autor nicht nachvollziehbar ist. Für entsprechende Hinweise wäre ich dankbar.
[1] Deutsche Wikipedia: Gottfried Wilhelm Leibniz (Link)
[2] Englische Wikipedia: Gottfried Wilhelm Leibniz (Link)
[3] George Boole: "The Calculus of Logic" 1848 (PDF) - Quelle verloren
[4] Deutsche Wikipedia: George Boole (Link)
[5] Leibniz Binärsystem, Auszug aus [6] Seite 86 in den verschiedensprachigen Wikipedien (aber mit zwei Druckfehlern) (PNG)
[6] Gottfried Wilhelm Leibniz: "Explication de l'aritmètique binaire" - französisches Original (PDF) - Auszug aus [7] ab Seite 255 mit nur einem Druckfehler 0101 = 13 statt 1101 = 13.
[7] Google-Books: Geschichte der königlichen Akademie der Wissenschaften zu Paris, 1703. 662 Seiten, 30 MB (Link) (abgedruckt 1705). Dort ab Seite 255.
[8] Gottfried-Wilhelm-Leibniz-Gesellschaft Hannover (Link)
[9] Heinz, G.: - Übersetzung der "Erläuterung zur binären Aritmetik" (Explication de l'aritmètique binaire) von Gottfried Wilhelm Leibniz (HTML), (PDF)
[10] Wikipedia: Karnough-Tafel
[11] G.W.Leibniz: "Linien von Fohy" oder später auch Ching-Hexagramm genannt, Leibnizsches Original (JPG)
[12] George Boole: "The Mathematical Analysis of Logic". Cambridge: Macmillan, Barclay & Macmillan; London: G. Bell, 1847. (PDF)
[13] Aus dem Altfranzösischen übersetzt mit https://translate.google.com mit manuellen Korrekturen
[14] Wikipedia: Zum konfuzianischen " Buch der Wandlungen - Yijing"
[15] Wikipedia:
Die dreizehn Klassiker konfuzianischer Prägung
Created 2023/02/23.
Editions: 2024/01/24, 2025/01/10
Source: http://www.gheinz.de/news/leibniz.htm
Mail to info@gheinz.de
Visitors since Dez.6, 2021: