Interferenzanalysen von Elektrocorticogrammen (ECoG)
Gerd Heinz
Können wir durch Nerven sehen? Es sollte untersucht werden, ob es mit interferenziellen Methoden möglich sein würde, durch Nerven zu 'sehen'. 30-kanalige ECoG-Aufnahmen wurden dafür von der Charité Berlin zur Verfügung gestellt.
Die Idee dahinter: Ich schaue mir einen Baum an. Ähnlich einer optischen Abbildung wird dieses Bild von den Augen über Nervenleitbahnen in den visuellen Cortex transportiert. Auch Berührungen oder Vorstellungen werden vom Nervensystem als Bilder transportiert.
Könnte es möglich sein, daß in ECoG-Daten Reste dieser Bilder enthalten sind und rekonstruiert werden können?
Die Antwort können nur Interferenzintegrale geben.
Mit Interferenzintegralen können wir im Nervensystem zweierlei berechnen. Zum einen die Erregungskarte (die des generierenden Raumes), zum andern die Zielkarte (die des detektierenden Raumes). Beide sind über eine Inversion der Zeitfunktionen verbunden.
Interferenzintegrale können also auf zwei unterschiedlichen Wegen bestimmt werden. Einerseits ist es möglich, sie als Interferenzrekonstruktion in der Form f(t+τ) zu rechnen, so wie dies bei der Entwicklung der akustischen Kamera parallel hierzu erfolgte. Dabei schauen wir in den erregenden Generatorraum zurück. Die entwickelten Bilder erscheinen seitenrichtig.
Andereseits ist es möglich, den Raum zu berechnen, in den die Zeitfunktionen fließen, in den Detektorraum. Das wäre in der Form f(t-τ). Hier entstehen im Ergebnis spiegelverkehrte Bilder.
PSI-Tools konnte beides. Durch eine zeitliche Inversion der Zeitfunktionen (Kanaldaten) vor Beginn der Rechnung konnte die standardmäßige Rekonstruktion in eine Interferenzprojektion überführt werden.
Merke:
Weil die Zeit immer vorwärts läuft und erst mit dem Computer invertiert werden konnte, konnte man vorher eigentlich nur Projektionen ausführen. Aber mit einem Trick hätte es gelingen können, auch mit Harware eine seitenrichtig kartierende Rekonstruktion zu entwickeln (sog. Beamforming in der Akustik oder Phased Arrays in der Radartechnik). Wenn man ein konstantes Delay T in allen, zu berechnenden Pfaden addiert, welches größer als alle τ ist, ergibt sich eine Form f(t-T+τ). (Addition eines Delays ist f(t-τ); Subtraktion ist f(t+τ)). Ob dies gelang, konnte der Author bis heute nicht zweifelsfrei klären. Im WWW wimmelt es von unverstandenen und falsch abgeschriebenen Beamforming-Formeln...
Siehe dazu auch diese Seite zu PSI-Tools.
Vorab wäre noch die Beantwortung der Frage wichtig, warum dieses Material damals nicht veröffentlicht wurde. Einerseits war der Zufall schuld, denn wir kamen mit akustischen Bildern schneller voran. 1997 waren schon erste Reporter und Fernsehteams da, aber nicht wegen ECoG-Aufnahmen, sondern wegen Schallbildern. Und dann lief uns auch schon die Zeit davon.
Das Problem: EEG/ECoG-Geräte hatten damals recht geringe Datenraten im Bereich um 2 kSps. Mit der Entwicklung schnellerer Datenrecorder mit eine Samplerate oberhalb von 50.000 Samples pro Sekunde (50 kSps) war die Hoffnung verbunden, Reste von Spikeaktivität im Datenmaterial zu finden und kartieren zu können. Diese Hoffnung bestätigte sich nicht.
Andererseits sind die für ein Verständnis nötigen Filmchen kaum in eine Druckvorlage zu quetschen. Auch war das Internet neu und es existierte die Vision, elektronische Medien würden über kurz oder lang ohnehin die gedruckte Form ablösen.
Nicht zuletzt war das Projekt NEURO3D (1995_Neuro3d.pdf) ausgelaufen. Nur in diesem Projekt ging es um zweigleisige Untersuchungen zu neuronalen und akustischen Interferenzrämen. In Folgeprojekten waren nur noch akustische Themen erfolgreich.
Etwa ein Dutzend Projektskizzen zu neuronalen Fragestellungen bei BMBF, wie BMWi, wie DFG wurden abgelehnt. Es gelang noch nicht einmal, Fördermittel für Neuroforschungen auf diesem Gebiet zu aquirieren. Bei DFG und BMBF wurde die GFaI in Projekten nur als Mitläufer geduldet, beim BMWi fördert man keine Grundlagenforschung. Als Einzelperson hat man sowieso keine Chance auf Förderung. Und so verstauben diese einmaligen Ansätze seit Jahrzehnten. Wie sagte schon Heine:
"Denk ich an Deutschland in der Nacht,
dann bin ich um den Schlaf gebracht."
Allerdings ist auch Selbstkritik angesagt. Ich verstand es damals nicht, den Stoff so locker, luftig und leicht darzustellen, daß Fördermittelzuwender etwas damit anfangen konnten. Wie leicht hatten es dagegen die ersten, akustischen Bilder: Diese verstand jeder.
Der Jenenser Psychiater Hans Berger registrierte 1929 mit einem Saitengalvanometer das erste Elektroenzephalogramm (EEG) eines Menschen. Die Fachwelt zweifelte an der Echtheit der registrierten Schwankungen im Mikrovolt-Bereich. Erst durch Verifikationen des Cambridge-Professors E. D. Adrian wurde diese Technik 1934 popularisiert. Bislang wurde aus der Sicht der Informatik wenig hinterfragt, welche ursächlichen Bewegungen die merkwürdigen EEG-Schwankungen verursachen. Henderson's Dipolmethode [1] erscheint zwar genial, doch zugleich scheint es realitätsfern, einen im Gehirn kreisenden Dipol als Template für eine sehr komplexe Erkennungsaufgabe zu nutzen.
Der Autor untersuchte zwischen 1992 und 1996 Elektro-Encephalogramme (EEG) bzw. Elektro-Cortikogramme (ECoG) mit dem Ziel, der Informatik, die mit dynamischen Prozessen in neuronalen Laufzeiträumen verbunden ist, näher zu kommen. Simulationen zeigen, daß von Laufzeiträumen abgenommene Kanaldaten große Ähnlichkeit zu EEG-Daten haben (siehe Seite 'Simulationen'). Wenn wir EEG-Daten betrachten, so können wir sehr genau das zeitliche und örtliche Vorankommen bestimmter großer Wellen beobachten. Genau dieses beobachten wir auch in der Simulation.
Geben wir nun eine bestimmte Wellenausbreitungsgeschwindigkeit für die Rekonstruktion der Daten vor, wäre zu erwarten, daß Erregungen einzelner Punkte zu unterschiedlichen Zeiten an der Oberfläche erscheinen. In ihrer Summe bilden sie die oberflächliche Wellenlandschaft. Wir sehen dann nicht mehr nur die Gummimembran, die an definierten Orten durch Elektroden ausgelenkt wird, sondern wir können dann in Approximation das erregende Feld selbst zurückrechnen.
Um diesen Unterschied zu erfassen, stelle man sich ein völlig umhülltes Aquarium vor, von dessen Oberfläche 30 Sensoren den jeweiligen Wasserstand ablesen. Bringen Fische das Wasser in Bewegung, so besteht die Aufgabe interferentieller Rekonstruktion darin, aus der Kenntnis der Abtastwerte des Wasserstandes zu bestimmen, wo sich die bewegungsauslösenden Fische gerade befinden. Dazu benötigen wir zwangsläufig eine mediale Geschwindigkeit der Wellenausbreitung.
Der Ansatz, der an lernfähige Systeme gebunden ist, geht davon aus, daß in einem universell lernfähigen Netzwerk im Moment des Lernerns den Sensoren nicht bekannt sein kann, wo (in welchen Neuronen) gelernt wird. Folglich ist zu erwarten, daß jede sensorische (oder andere) Information, die u.U. in Zusammenhang mit anderen Informationen ein mögliches Lernen ergibt, in viele (oder besser in alle) Richtungen gestreut wird, in denen diese Information von Belang sein könnte. Je perfekter diese Streuung, umso perfekter ist das System in der Lage, scheinbar zusammenhanglose Informationen verschiedenenster Sensoren lernend zu verkoppeln. Dazu denke man an Turner oder Turmspringer: Hier ist es nötig, hunderte Muskelspannungen und Gelenkstellungen mit Informationen des Gleichgewichtsorgans, des Gehörs und des Sehens auf komlexestem Wege zu verkoppeln.

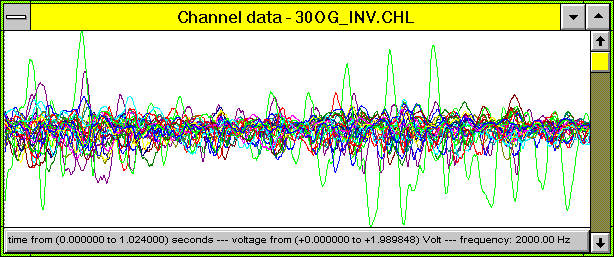
Bild 1: 30-Kanal ECoG der Charite, Quelle [2], Darstellung mit der Software Bio-Interface / PSI-Tools [5], [6].
Wenn also ein lernfähiges System hochwahrscheinlich Informationen in verschiedene Richtungen streut, dann sollte es auch gelingen, die Erregungen einzelner Neuronen aus der zeitkompensierten Korrelation von Kanaldaten zu ermitteln. Als mathematische Beschreibungsmittel steht uns z.B. die Kreuzkorrelation zweier Beobachtungspunkte zur Verfügung. Setzen wir voraus, daß sich jedes Signal mit endlicher Leitgeschwindigkeit fortpflanzt, und versehen wir beide ankommenden Zeitfunktionen mit einem zeitlichen Versatz, der den zeitlichen Abstand vom zu beobachtenden Ort jeweils kompensiert, so können wir anhand der Korrelationshöhe feststellen, wie stark beide nun kompensierten Zeitfunktionen miteinander harmonieren. Das Maß dieser Harmonie (das Ergebnis der Korrelation) erscheint uns als Maß für die Erregung dieses Punktes.
Setzen wir dieses Verfahren für alle anderen Punkte entlang der Verbindungslinie zwischen den zwei Elektroden fort, so erhalten wir für jeden Punkt einen Korrelationswert, der unter Vernachlässigung störender Einflüsse offenbar aussagt, wie stark dieser Punkt an der Bildung der an den Elektroden gemessenen Zeitfunktionen beteiligt war. Um nun über die Korrelationen entlang einer Linie zwischen zwei Punkten hinausgehend weitere Punkte des Raumes bestimmen zu können, benötigen wir zusätzliche Zeitfunktionen, die an anderen Orten aufgenommen wurden. Zur Bestimmung einer n-dimensionalen Punktwolke benötigen wir mindestens n+1 Zeitfunktionen (Kanäle). Die ursprüngliche Kreuzkorrelation wird erweitert. Im Integral zur Ermittlung des Korrelationswertes eines Punktes stehen jetzt mehr als zwei Zeitfunktionen: Jede aufgenommene Zeitfunktion wird mit dem zeitlichen Elektrodenabstand kompensiert aufgenommen. Den n-dimensionalen Vektor (n: Kanalzahl) der zeitlichen Abstände eines zu beobachtenden Punktes von den abtastenden Elektroden nennen wir Maske des Punktes.
Wird das Verfahren auf eine Vielzahl von Elektroden erweitert, so erhalten wir die Möglichkeit, die Korrelationen (Interferenzwerte) für alle Punkte des Raumes präziser zu bestimmen, je höher die nutzbare Kanalzahl ist. Das multiplikative Interferenzintegral eines Punktes stellt demgemaß ein verallgemeinertes Korrelationsprodukt mit mehreren Kanälen dar. Wohl aber zeigt sich, daß neben der multiplikativen Verknüpfung auch andere Verknüpfungsoperationen von Belang sind. Neuronale Lernmodelle nutzen nahezu ausschließlich die Addition zur Bewältigung eines vergleichbaren Problems, dem des Lernens.
Wir gehen (vereinfacht) von folgenden Annahmen aus:
1) Jede Elektrode nimmt die Summe aller Erregungen des Raumes auf (radial abklingend oder unbewertet);
2) Wenn sich eine Partialwelle von einem erregenden Punkt P herkommend ausbreitet, so erreicht sie verschieden entfernte Elektroden zu verschiedenen Zeiten.
3) Zur Rekonstruktion wird die n-kanalige Korrelation pro Zeitschritt berechnet. Es entsteht ein Interferenzwert des Punktes (in den Movies zu sehen). Aufsummiert (integriert) über die Zeit entsteht der integrale Interferenzwert dieses Punktes, der ein Maß für die von diesem Punkt ausgegangene Erregung ist.
Das Verfahren wurde zunächst für experimentelle Simulationen verschiedener Laufzeiträume (neuronal, akustisch, optisch) entwickelt. Die Anwendung für EEG/ECoG-Aufnahmen steht vor der Unsicherheit, daß uns im Moment noch zu wenig über Geschwindigkeitseigenschaften des Mediums bekannt ist. Da aber die Überprüfung dieser Fragen mit Mitteln der Interferenz zwangsläufig einen Erkenntnisgewinn mit sich bringen wird (und auch nur so möglich ist), erscheint uns die experimentelle Überprüfung als legitim.
Eine Analyse eines unter der Schädeldecke 30-kanalig aufgenommenen Elektro-Cortikogramms (ECoG) zeigt, daß es sich bei den aufgenommenen Daten um Ableitungen aus einem kontinuierlichen Wellenraum handeln könnte.
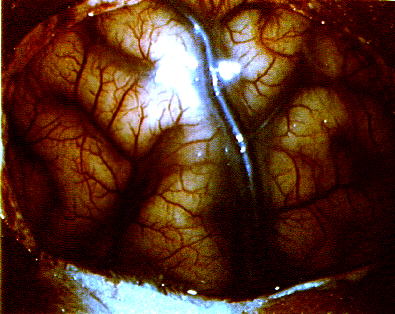
Bild 2: Die Folie mit dem Elektrodenarray wird beim Elektrocortikogramm (ECoG) unter die Schädeldecke gelegt. Quelle [4]
Unter einer vereinfachenden Annahme homogener Ausbreitung neuronaler Aktivität in Form konzentrisch auseinanderlaufender Wellen nimmt eine ECoG-Elektrode die Summe aller Aktivitäten der Umgebung auf, wobei jede Aktivität zeitlich verzögert um den Abstand von der Elektrode an ebendieser erscheint. Folglich, so die Hypothese, wären ECoG-Kurven die Aufnahme der Auslenkung eines resultierenden Wellenfeldes an einem spezifischen Ort.
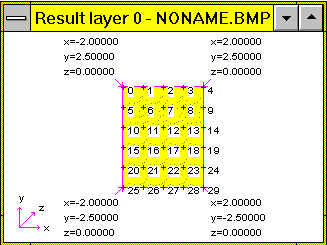
Bild 3: Elektrodenanordnung von oben dargestellt (alle Maße in cm)
Da vergleichbar zur Optik jede Verbiegung eines Laufzeitraumes durch fehlerhafte Bilder bestraft wird, sind die 30 Elektroden zur numerischen Rekonstruktion auf der Oberfläche eines Ellipsoids angeordnet.
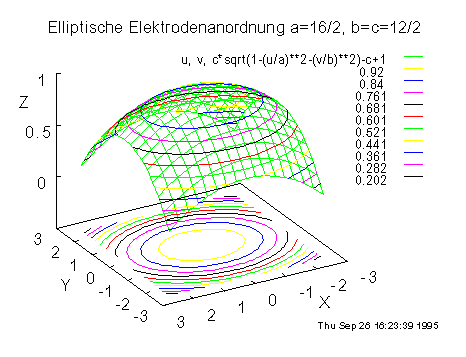
Bild 4: Sphärisches Modell der Elektrodenanordnung. Die exakte Vermessung der Lage der Elektroden bestimmt das Rekonstruktionsergebnis wesentlich.
Das uns der Gedanke eines Wellenkontinuums in Interferenzanalysen aus ECoGs zunächst vermessen erschien, erklärt die Tatsache, daß wir bereits am 26.9.95 erste Integrale dieser Wellenfelder berechneten (mehrkanalige Korrellationsprodukte für alle Raumpunkte), aber nur interessehalber, quasi zur Abrundung der Experimente erst am 6.10.95 ein Movie des Wellenfeldes selbst machten. Zur Begründung sei angemerkt, daß die zugrunde liegende Interferenztransformation (HIT) für schwach besetzte Kanäle entwickelt wurde (dort auch funktioniert), daß es aber im Bereich stark besetzter Kanäle noch einige Probleme gibt. Die HIT ist ein Approximationsverfahren, das unter der Voraussetzung schwach besetzter Kanäle oder hoher Kanalzahlen gut gegen die Lösung konvergiert. Dies läßt sich in Simulationen (siehe nebenstehende Page) zeigen. Gleichzeitig läßt sich aber auch zeigen, daß unter bestimmten Bedingungen (stark besetzte Kanäle bei geringer Kanalzahl) Phantomerregung auftritt. In den GH-Simulationen charakterisiert diese die Störungen am Bildrand. Bei den uns zur Verfügung stehenden ECoG-Daten sind aber kaum Randwerte bekannt, sodaß die Qualität der Aufnahmen im Moment nicht abschätzbar ist. Umso erstaunter waren wir, als am 6.10.95 aus einem 30-kanaligen ECoG folgende Videos berechnet wurden, die nicht ein erwartetes Chaos zeigen.
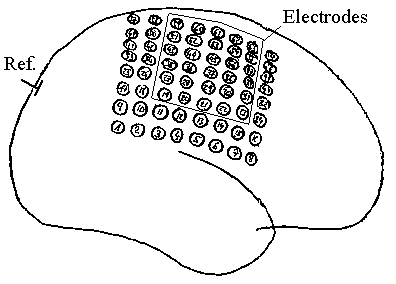
Bild 5: Elektrodenanordnung auf dem Pallium. Die Elektroden sind auf einer flexiblen Folie im Raster von 1 cm angeordnet, Quelle [4].
Die Aufnahmen sind nicht mit Tomographie-Aufnahmen zu verwechseln. Der Versuch, aus den Kanaldaten über Interferenz die makroskopische Hirnstruktur abzuleiten, scheiterte vollständig. Was wir folgend sehen, ist eine Abbildung eines mehrdimensionalen, inhomogen vernetzten Erregungsraumes auf einen dreidimensionalen, virtuellen, homogen vernetzten Rekonstruktionsraum. Es wäre möglich, daß bestimmte Konturen völlig anderen, weit entfernt liegenden Organen zuordenbar sind, deren Bild in den Aufnahmeraum projiziert wird. Es lag die Hoffnung zugrunde, daß sich in ECoG-Daten winzige Reste von Spike-Aktivität befinden, die vom Algorithmus wieder ans Tageslicht gebracht werden können.
(Alle Auswertungen erfolgten mit dem Bio-Interface / PSI-Tools [5], [6])
Erste Sekunde schläfriger Hirnaktivität, gemessen auf einer Pallium-Fläche von 5 x 6 cm². Erste, noch unvollkommene Bilder elektrischer Hirnaktivität aus dem 30-Kanal-ECoG eines Epilepsieherdes. Movies vom 6.10.1995 berechnet an der GFaI Berlin. Alle Zeitfunktionen werden ohne Kontrastverschärfung entsprechend ihrer Maske zueinander addiert. Die Kanaldaten sind von der Schwankung der Referenzelektrode befreit (Gleichtaktbefreit) und symmetriert. Der virtuelle Laufzeitraum zur Rekonstruktion ist auf eine homogene Ausbreitungsgeschwindigkeit von 1 Meter pro Sekunde eingestellt. Die Bildfrequenz ist in allen Aufnahmen identisch zur Samplefrequenz der Kanäle von 2 kHz gewählt.
Die ECoG-Daten entstammen einem Epilepsie-Herd der rechten Hemisphäre. Die Elektroden sind unter die geöffnete Schädeldecke geschoben. Die dargestellte Rechen-Ebene liegt konzentrisch unter den ellipsoid auf die Hirnhaut gelegten Elektroden im Abstand von 0...6mm. Man beachte die zusammenhängende Ausbreitung von Gebieten niederer Aktivität. Bemerkenswert an diesen Aufnahmen ist deren Qualität. Erst im Nachgang vorgenommene Auswertungen von Kanaldaten aus dem (eigentlich idealen) Laufzeitraum der Akustik zeigen, daß im Bereich der ECoG-Auswertungen unerwartet glatte Interferenzbilder entstehen. Eine Deutung dieses Phänomens könnte die sein, daß das Gehirn offenbar mehr als erwartet Eigenschaften eines Laufzeitraumes im Geschwindigkeitsbereich von 0,5 m/s bis 2 m/s besitzt. Dies stützt eine Annahme über den Entstehungsmechanismus evocierter Potentiale: Man nimmt an, daß die äußerlich meßbare Summenaktivität im wesentlichen synaptische Aktivität, nicht aber die Impulsaktivität der Neurone widerspiegelt [3].
Bild 6: Movie 1 MB, Aufnahmedauer 0.29 Sekunden bei 2 kHz Bild- und Abtastfrequenz; 576 Bilder. Click the image to download the *.avi-file. Configure MS-Windows mplayer.exe to inspect *.avi-files using 'Video for Windows'
Das Wellenfeld wurde mit einer verringerten Hintergrundgeschwindigkeit (0,75m/s) und höherer Auflösung rekonstruiert. Vergleichbar zur Rekonstruktion mit 1m/s erscheint dadurch ein größerer Bildausschnitt.
Dadurch, daß zur Rekonstruktion zunächst ein homogener Laufzeitraum angenommen wird, rekonstruiert der Algorithmus die Daten auch so, als kämen sie aus einem solchen. Der Algorithmus weiß nicht, daß bestimmte Elektroden durch Furchen von entsprechenden Bildpunkten getrennt sind. Damit gehen strukturelle Informationen zunächst verloren. Derzeit arbeiten wir daran, diese strukturellen Informationen der Zuordnung von Elektroden zu Bildpunkten vorab zu ermitteln, um anschließend die Rekonstruktion im diskontinuierlichen Raum durchführen zu können.
Man beachte, wie sich ein Fleck (vermeintlich) starker Aktivität (blau) oft kontinuierlich über mehrere Elektroden verschiebt. Offenbar sind Flecken hoher Aktivität eingehüllt von zumeist geschlossenen Ringen verminderter Aktivität (gelb). Der Eindruck, alle Information käme aus dem Hirnzentrum täuscht. Diskontinuitäten an den Rändern führen zu einem allgemein geringeren Interferenzniveau der Außenelektroden. Würden weitere Wellenfelder aus dem Außenbereich wirken, könnte dieser Eindruck verloren gehen.
Bei der Berechnung der Wellenfelder entdeckten wir eine interessante Eigenschaft, die uns zunächst als ein Fehler in der Versuchsdurchführung erschien. Rekonstruiert man die Kanaldaten in zeitlich geordneter Reihenfolge vorwärts, entsteht ein rückwärtslaufender Film des Wellenfeldes. Simulationen einzelner Wellenausbreitungen zeigen, daß dies prinzipiell so ist (siehe dort). Die Abspielrichtung obiger Aufnahmen wurde deshalb nachträglich korrigiert. Es entsteht dann ein Problem, wenn ein kontinuierlicher Datenstrom online rekonstruiert werden soll: Die Zeit im Wellenraum läuft zwangsläufig vom Startzeitpunkt aus rückwärts. Offenbar haben wir es mit einer höchst bemerkenswerten Eigenschaft der Dimension "Zeit" der virtuellen Wellen der Interferenzrekonstruktion zu tun.
So erfreulich diese ersten Eindrücke sind, so ist uns doch bewußt, daß die Bilder erst einen Anfang kennzeichnen. Es wäre zum gegenwärtigen Zeitpunkt vermessen, an einen klinischen Einsatz dieses Verfahrens zu denken. Verschiedene Eigenschaften der Interferenztransformation sind noch unbekannt. Das Konvergenzverhalten dieses Approximationsverfahrens für immer dichter werdende Kanaldaten ist zu untersuchen. Fehlermechanismen sind zu erkennen und zu beseitigen. Simulative Verifikationsverfahren sind zu entwickeln bzw. zu verfeinern. Es sind gedankliche Modelle zu entwickeln, die ein Verständnis für den vor uns liegenden, inhomogenen, mehrdimensionalen Raum gestatten. Interessante Leitgeschwindigkeiten sind zu bestimmen. Die Geschwindigkeitsklasse, aus der das Bild hauptsächlich entsteht, ist zu ermitteln. Die Überlagerung der einzelnen, in die Kanaldaten eingehenden Geschwindigkeitsklassen ist zu trennen, Strukturelle Gliederungen sind zu ermitteln, die Aufnahmen sind zu verifizieren.
Eine statische Analyse ('Gummimembran') eines 30-kanaligen ECoG-Datensatzes zeigt Bilder, die äußerlich vergleichbar zu Dipol-Rekonstruktionen sind. Ausgangspunkt ist hier ein einziges Sample aller Kanaldaten pro Zeitschritt, dessen Amplitude als Farbwert den Elektrodenpositionen zugeordnet wird. Die Werte zwischen den Elektroden können in geeigneter Weise über Splines interpoliert werden. Für das folgende Movie nutzten wir den Interferenz-Simulator, und stellten lediglich die zur Rekonstruktion nötige Leitgeschwindigkeit auf einen sehr hohen Wert ein, der der ionisch-elektrischen Ausbreitung nahe kommt (>10000 m/s), sodaß infolge der zu niederfrequent abgetasteten Kanaldaten Interferenzen praktisch keine Rolle mehr spielen.
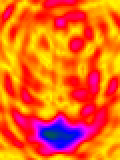
Bild 7: Rekonstruktion einer nichtinvasiv aufgenommenen EEG-Ableitung, Schnittebene horizontal in Augenhöhe. Interessant ist der mittig-senkrechte Artefakt, der eigentlich einer Erklärung bedarf.
Bild 8: Filmausschnitt einer statischen Rekonstruktion (mit unendlich hoher Leitgeschwindigkeit, *.avi, 100 kB) mit maximalem Farbkontrast pro Bild
Die so erhaltene statische Rekonstruktion funktioniert natürlich nur dann, wenn der elektrodische Wirkungsradius durch eine geeignete Funktion (z.B. Gauss) mit der Entfernung abklingt. Hingegen ist für interferenzielle Rekonstruktionen nicht unbedingt ein Abklingradius erforderlich. Obige Interferenzaufnahmen wurden ohne diesen berechnet.
Bei der Wahl der Rekonstruktionsgeschwindigkeit gibt es nur Vermutungen. Könnte es sein, daß der Algorithmus so stark ist, um bei verschiedenen Rkonstruktionsgeschwindigkeiten unterschiedliche nervliche Aktivitäten zu rekonstruieren? Wir näherten uns dem Thema mit einigen Versuchen, deren Ergebnisse noch nicht wirklich überzeugen konnten.
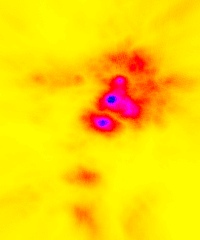
Bild 9: 30-Kanal-Interferenzintegral aus dem ECoG eines Epilepsieherdes über die Länge eines Datensatzes von 3 Sekunden integriert. Die laterale Ausbreitungsgeschwindigkeit wurde hier mit 50 cm/sec gewählt. Blau: starke, gelb: geringe Aktivität
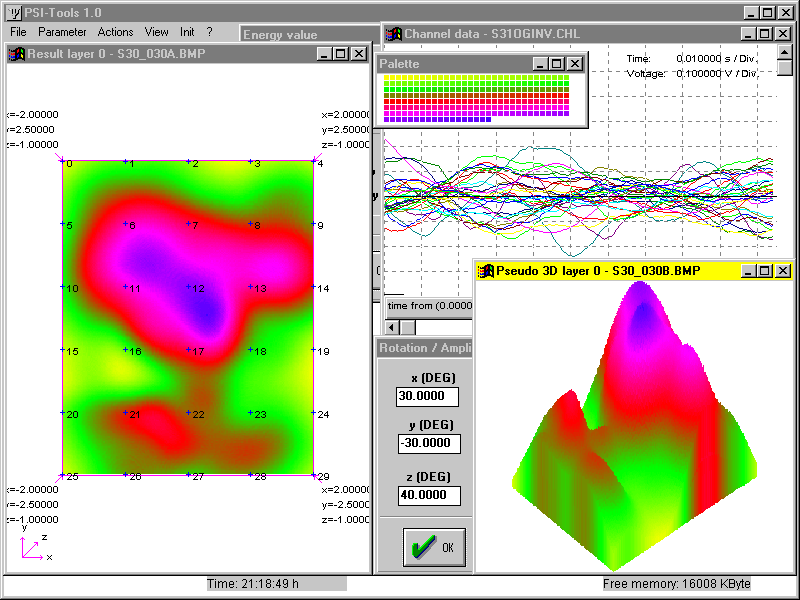
Bild 10: Windows-Oberfläche von PSI-Tools. Rekonstruktion aus einer ECoG-Ableitung, Schnittebene horizontal, 1cm unter den Randelektroden, Integral über 1sec., 2kHz, 30cm/s
Bislang wissen wir nicht, welche Leitgeschwindigkeit optimale Ergebnisse liefert, d.h. welches der interessanteste Geschwindigkeitsanteil ist, der die Ausbildung von ECoG-Kanaldaten am wesentlichsten beeinflußt. In folgenden, integralen Untersuchungen fällt auf, daß die Geschwindigkeiten 12 cm/s und 40 cm/s Maxima im Interferenzwert liefern.
Sabine Höfs variierte verschiedene Parameter. Es entstand eine ganze Serie von Aufnahmen, die in einem separaten Aufsatz zu finden sind:
Zum Aufsatz zu Geschwindigkeitsvariationen (speedzm.htm)
Hier liegen noch einige Filmchen von Geschwindigkeitsvariationen (alle Bildfolgen 2048 Hz, zeitlich nicht invertiert):
Rekonstruktion mit 2 m/sec (243 kB)
Rekonstruktion mit 5 m/sec(254 kB)
Rekonstruktion mit 10 m/sec(254 kB)
Es fällt auf, daß die Filme allesamt informationsarm wirken. Deshalb interessierten wir uns im nächsten Schritt nur für bestimmte Teilmengen der Rekonstruktion.
PSI-Tools gestattet es, die Rekonstruktionseben in verschiedene Tiefen zu legen (analog zur Entfernungseinstellung der akustischen Kamera). Nicht verwunderlich entstehen verschiedene Bilder.

Bild 11: Rekonstruktion des Tiefenprofils einer 30-Kanal-ECoG-Ableitung (Angaben in mm unter elliptischer Oberfläche, siehe oben).
Leider ging der Initialisierungsfile zu dieser Aufnahmenserie verloren. So läßt sich weder sagen, mit welcher Geschwindigkeit, noch mit welchen sonstigen Parametern die Aufnahme gemacht wurde. Es scheint fast, als ob hier nur ein eingegrenzter Bereich (eine Klasse) von Interferenzwerten dargestellt wurde.
Eigentlich hatte ich die Hoffnung schon aufgegeben, aus ECoG-Aufnahmen noch irgendwelche brauchbaren Informationen ziehen zu können. Spikes waren nicht vorhanden. Das monotone Gewaber der Wellen machte müde. Aber dann implementierten wir für irgendeinen Debug-Zweck eine Klassenanalyse. Die genauen Umstände, die zu dieser Idee führten, gingen leider verloren. Offenbar waren sie von so banaler Art, daß es nicht lohnte, die Dinge abzuspeichern.
Bei der Klassenanalyse werden im Gegensatz zum gewöhnlichen Interferenzintegral nur die Werte in das Integral aufgenommen, die innerhalb einer Werteklasse liegen. Die Summe der Bildpunktwerte aller Klassen ergibt dann wieder das Integralbild.
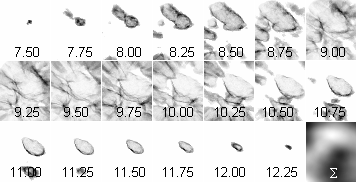
Bild 12: Faszinierendes Integral des Wellenfeldes bei einer Hintergrundgeschwindigkeit von 50 cm/sec aufgeteilt auf verschiedene Interferenzwertklassen der Breite 0.25, beginnend mit 7.50 über eine Laufzeit von einer Sekunde. Kanaldaten mit erhöhter 3Hz-Spikeaktivität (File s31ogvi.chl).
Unerwartet zeigte die Klassenanalyse der Interferenzrekonstruktion (Bild 12) zusammenhängende, scharfe Strukturen, die nicht wie Wellen aussehen. Merkwürdigerweise zeigt dann aber das Summenbild dieselbe, charakteristische Unschärfe, wie die Wellenbilder. Als Ursache der wachsenden, integralen Unschärfe werden Zoom-Effekte angenommen, die durch eine Modulation der Leitgeschwindigkeit in größeren Arealen entstehen. Die Differenzierung der Rekonstruktionen nach Interferenzwertklassen zeigt erstaunlich zusammenhängende Graphen, die allerdings in der Addition aller Klassen zum Summenbild verschwinden.
Im folgenden Movie (Bild 13) wurde eine Aufnahme gemacht, die relativ niedrige Interferenzwerte enthält. Man beachte einige statisch feststehende Figuren des Movies. Leider sind die Details in Vergessenheit geraten (2019), siehe dazu die letzte Möglichkeit zum Download der Software [5] sowie des Datensatzes [6].
Bild 13: Ausschnitt einer Klassenanalyse eines 30-Kanal ECoG entlang des Homunculus (Quelle: Charité, PD Dr. Bartsch, Herr Krüger 1995 [2]). Sehen wir hier einen Wellenfilm? Wohl kaum. Es scheint, als würden wir durch die Nervenstränge auf Körperteile schauen, gerade so, wie es im Buch Neuronale Interferenzen dargestellt ist. Nur noch wenig ist über Details bekannt. Algorithmus: Addition, Klasse der Interferenzwerte von 0 bis 0.5, Kanaldaten s31oginv.chl, 2kHz, Beginn mit Samples 0-100, in 10-er Schritten weiter, zeitlicher Abstand zwischen den Aufnahmen 5 Millisekunden.
Bislang ist eine Deutung dieser Aufnahmen nicht möglich. In ihrer Schönheit und Mystik liegt ein Geheimnis. Leider kam damals irgendein hochwichtiger Meßauftrag dazwischen und die Sache geriet für Jahre in Vergessenheit. Könnte mich heute noch ärgern. Habe einige Zeit verwendet, um Einstellungen für eine Verifikation dieser Aufnahme zu finden. Leider bislang vergebens.
Es kann angenommen werden, daß hohe Interferenzwerte durch Grundpotentiale (Glia) entstehen, daß aber die eigentlich interessanten Informationen eine Modulation dieser Grundpotentiale sind. Verwunderlich ist der scheinbar enorm plastische Eindruck dieser Aufnahmen. Hohe Interferenzwerte korrespondieren zu dunkler Färbung. In PSI-Tools ließ sich die Integrationszeit einstellen. Eine Deutung wäre, daß eine relativ hohe Integrationszeit pro Pixel gewählt war und kleine darüberlaufende Wellen die Integrale nicht wesentlich veränderten. Auch gibt die "Klassenanalyse" Rätsel auf. Sabine Höfs hatte sie gerade erst implementiert, aber die Entwicklung wurde abrupt abgebrochen. Die Idee dahinter ging verloren.
So sehen wir erstaunlich markante Bilder, haben aber eigentlich bis heute (2020) keine Erklärung dafür. Nur eines ist sicher: Wird eine Erklärung gefunden, dann wird der EEG-Spezialist lieber Bilder, als Zeitfunktionen interpretieren. Und ein Nobel-Preis liegt wohl in der Nähe.
Wir sehen: Hier ist noch ein wenig Grundlagenforschung zu leisten. Sie können eigene Experimente machen mit einem 30-Kanal-ECoG-Datensatz incl. INI-File (gezippt, 234 kB) für PSI-Tools [5], [6]. Ob dieser File indes den oben bezeichnete File s31oginv.chl darstellt, ist in Vergessenheit geraten.
Aber werden sie nicht übermütig. Vom deutschen Staat wird nur etablierte Grundlagenforschung mit Milliarden Euro subventioniert (Quantenphysik, Kosmosforschung, Materialforschung etc.). Nur etablierte, "gemeinnützige" Institutionen haben Lobbyorganisationen und sind antragsberechtigt. Mittel für Ideen kleiner Entdecker oder Erfinder aber fehlen vollständig. Erfindungen machen stets Individuen - aber Nutznießer ist in DE immer das Kollektiv! Vergeuden Sie deshalb keine Zeit mit Förderanträgen (ich vergeudete viel Zeit meines Lebens damit) und sprechen Sie lieber private Stiftungen an.
Weil die Klassenanalyse in der Rekonstruktion des generierenden Raumes so erfolgreich war, könnte auch die Projektion in den detektierenden Raum (Cortex) erfolgreich sein? Um dieser Frage nachzugehen, invertieren wir die Zeitfunktionen zeitlich mit PSI-Tools.
Seit 5/97 ist es mit PSI-Tools möglich, auch Serien kurzer, teilüberlappender Interferenzintegrale zu berechnen. (Damit entstanden die akustischen Movies, zu sehen auf den verschiedenen Akustik-Seiten). Analog zur Rekonstruktion akustischer Wellenfelder wird die Integrationszeit so lang gewählt, wie eine Welle braucht, um das Detektorfeld zu passieren. Im Bild bleibt dann nur der Abdruck hoher Interferenzen zwischen verschiedenen Wellen stehen.
Das Problem besteht im Gegensatz zur Akustik darin, daß die zu detektierende Leitgeschwindigkeit unbekannt ist. In der Literatur finden wir eine Vielfalt von möglichen Leitgeschwindigkeiten, siehe 1994_IWK.pdf.
Mit den Aufnahmen sollte die Frage beantwortet werden, ob genügend hohe Potentiale mit Ionengeschwindigkeit transportiert werden, sodaß interferenzielle Analysen auch bei ECOGs nutzbar werden. Die Frage könnte bejaht werden, wenn wir eindeutige Interferenzorte finden, deren topographische Kartierung erstens stehen bleibt (und nicht über das Bild läuft) und zweitens in Relation mit den Hirnwindungen steht. Hier also erste Ergebnisse.
Bild 14: Interferenzrekonstruktion mit zugehörigem PSI-Tools Ini-File.
Als Ausbreitungsgeschwindigkeit wurde zunächst 10 cm/s angenommen. Das Bildfeld ist 1 cm unter der Oberfläche gesetzt. Pro Bild ist eine Integrationsdauer von 0,125 Sekunden eingestellt. Die Rekonstruktion erfolgte mit einer Frequenz von 400 Bildern pro Sekunde.
Sonstige Daten: Effektivwertbildung, Kanaldatenfile: s31oginv.chl, 2000 Sps über 1500 Samples. Rechenzeit ca. 10 Stunden auf Pentium 130.
In der Aufnahme ist eine Restwelligkeit zu erkennen. Auch läßt die Schärfe zu wünschen übrig. Eine eingeschaltete automatische Farbanpassung sorgt für gleichbleibend maximalen Palettenkontrast, damit werden zeitliche Amplitudenveränderungen leider nicht sichtbar.
Mit dem max-Operator begrenzen wir das Gewabere von kleinen Emissionen des Wellenfeldes, daß wir eigentlich nicht im Bild haben wollen. Folgende Aufnahme entstand mit erhöhter Hintergrundgeschwindigkeit von 20 cm/s und mit Maximum-Operator. Die automatische Kontrastmaximierung ist ausgeschaltet.
Bild 15: Interferenzrekonstruktion. Daten: Maximum, Bildrate 10 Samples = 200 Bilder pro Sekunde, Mediale Geschwindigkeit 20cm/s, Algorithmus: Maximum, Rechenebene eliptisch (siehe oben), Integrallänge pro Bild 100 Samples = 50ms, Bildabstand 10 Samples = 5 ms, Kanaldaten s4_0.chl, time revers, 2kSpS, Initialisierungsdaten Ini-File, Movie 1,9MB
Es fällt auf, daß stets die Mitte höchste Integralwerte bekommt. Dies ist wohl mit der endlichen Ausdehnung des Arrays zu erklären. Auch wenn erste, stehende Bildteile sichtbar werden, befriedigen diese Ergebnisse nicht. Als sinnvoll kann ein Interferenzbild erst dann angesehen werden, wenn wenigstens kleine Bereiche existieren, die unerregt bleiben (Furchen etc.), siehe Klassenanalyse.
Während wir bei der interferenziellen Rekonstruktion davon ausgehen, einen Laufzeitraum zu beobachten und dessen Erregungsorte zu rekonstruieren, wollen wir nun eine zweite Möglichkeit diskutieren.
Angenommen, die an den ECoG-Elektroden zu messende Erregung stammt vornehmlich von Axonen aus tieferen Regionen des Hirns (Thalamus etc.). Angenommen auch, die Interferenztransformation ist hinreichend selektiv, um sich nur für den zu berechnenden Raum zu interessieren und fremde Signalanteile werden hinreichen unterdrückt.
Dann ist es legitim, mit dem Interferenzanalysator das Pallium nachzubilden und nach Orten zu fragen, deren Erregung sehr hoch wird. Zum Zweck der Berechnung von Projektionen besitzt PSI-Tools eine Zeitumkehrung: mit der 'time revers'-Funktion lassen sich die Kanaldaten zeitlich invertieren. PSI-Tools berechnet dann die Projektion desselben Detektorraumes. Siehe auch die Simulations-Seiten, um die Wirkung der verschiedenen Verfahren zu verstehen. Hier erste Ergebnisse.
Bild 16: Interferenzprojektion. Daten: Effektivwert, Bildrate 10 Samples = 200 Bilder pro Sekunde, Mediale Geschwindigkeit 20cm/s, Algorithmus: Maximum, Rechenebene eliptisch (siehe oben), Integrallänge pro Bild 1000 Samples = 500ms, Bildabstand 10 Samples = 5 ms, Kanaldaten rev_s4_0.chl, time revers, 2kSpS, Initialisierungsdaten Ini-File. Ergebnis vom 5.August 1997
Bild 17: Interferenzprojektion. Daten: Effektivwert, Bildrate 10 Samples = 200 Bilder pro Sekunde, Mediale Geschwindigkeit 20cm/s, Algorithmus: Maximum, Rechenebene eliptisch (siehe oben), Integrallänge pro Bild 100 Samples = 50ms, Bildabstand 10 Samples = 5 ms, Kanaldaten rev_s4_0.chl, time revers, 2kSpS, Initialisierungsdaten Ini-File. Ergebnis vom 5.August 1997
Partiell atmet das Wellenfeld, die Bilder sind unscharf, die Interferenzorte erscheinen matschig. Aber es ist unzweifelhaft, daß die Interferenzorte im Vergleich zur Rekonstruktion zum Stehen gekommen sind. Die zu entdeckenden Fensterkreuze am Anfang der Aufnahme interpretieren wir als Gleichtaktstörung auf allen Kanälen, die vor Rechenbeginn ausgefiltert werden kann. Der zur Verfügung stehende Datensatz hat eine noch zu geringe Bandbreite. Künftige Aufnahmen werden mit Datensätzen erfolgen müssen, die mit höheren Sampleraten aufgenommen werden. Auch könnten verkleinerte Elektrodenmatrizen erheblichen Zuwachs der Aussagemöglichkeiten bringen.
Sollten Sie eigene Untersuchungen auf der für alle Experimente benutzten Software Bio-Interface alias PSI-Tools durchführen wollen, bitte senden Sie eine Mail. Ich bin interessiert daran, mich mit Partnern über die erzielten Ergebnisse austauschen zu können.
Es sollte untersucht werden, ob es mit interferenziellen Methoden möglich sein würde, durch Nerven zu 'sehen'. ECoG-Aufnahmen dafür wurden von der Charité Berlin zur Verfügung gestellt.
Weder verschiedene Rekonstruktionen der 30-kanaligen ECoG-Daten, noch Projektionen konnten überzeugen. Eine Bestimmung einer optimalen Leitgeschwindigkeit war nicht zweifelsfrei möglich.
Einzig die Bilder einer zufällig gemachten, rekonstruktiven Klassenanalyse zeigen völlig unerwartet erstaunliche Details. Über deren Wesen aber besteht bis heute noch keine Klarheit.
Mein besonderer Dank gilt Sabine Höfs (geb. Schwanitz) für ihr außergewöhnliches Engagement bei der Entwicklung der hierfür genutzten Software "Bio-Interface" (später benannt in "PSI-Tools").
Vielen Dank für viele, wertvolle Informationen und für die Bereitstellung eines 30-Kanal Datensatzes an Herrn PD Dr. med. Peter Bartsch und Herrn Hartmut Krüger (Charité Berlin, Inst. f. Physiologie).
Dank an Herrn Dr. med. Torsten Griepentrog (Landesklinik Teupitz), mit dessen Hilfe am 16.12.1992 das Daumenexperiment (PDF), (HTML) gelang, daß den Anfang [9] dieser Entwicklung markierten sollte.
Dank auch an Dr. Manfred Lambertz (FU Berlin, Inst. für Physiologie), Prof. Dr. Vogel (Charité, Neurochirurgie) und an Dr. Raúl Rojas (Martin Luther Universität Halle/Freie Universität Berlin) für wertvolle Diskussionen, sowie an Peter Puschmann und Gunnar Schoel (Fachhochschule für Technik und Wirtschaft Berlin) für die gemeinsamen Experimente zum Nachweis neuronaler Elementarfunktionen mit deren PPN-Simulator [10].
Recht herzlichen Dank für die freundliche Unterstützung auch an den Geschäftsführer der GFaI, Herrn Dr. Hagen Tiedtke, sowie an den Vorstandsvorsitzenden der GFaI, Herrn Prof. Dr. Alfred Iwainsky.
Nicht zuletzt Dank auch an Diskussionspartner und Helfer in der Geburtsstunde theoretischer Grundlagen der "Neuronalen Interferenzen", Prof. Dr. Horst Völz (Freie Universität Berlin), Prof. Dr. Christian Hamann (Technische Fachhochschule Berlin) und Prof. Dr. Achim Sydow (GMD-FIRST Berlin).
[1] Henderson, C.J., Butler, S.R., Glass, A.: The Localization of Equivalent Dipoles of EEG Sources by the Application of Electrical Field Theory. Electroencephalography and Clinical Neurophysiology, Elsevier Sc. Publ. Comp. Amsterdam, 1975, 39 pp. 117-130
[2] Die ECoG-Datensätze (1995) stammten von PD Dr. med. Peter Bartsch und Hartmut Krüger aus dem Inst. f. Physiologie der Charité, Hessische Str. 3-4, 10115 Berlin
[3] Schmidt/Thews: Physiologie des Menschen, 24. Aufl., Springer 1990, S.142
[4] Foto mit Erlaubnis der Neurochirurgie der Charitè, Dr. Woiciechowsky, Prof. Vogel
[5] Download PSI-Tools gezippt. Funktioniert noch halbwegs unter WindowsXP.
[6] Download 30-Kanal-ECoG-Datensatz incl. INI-File (gezippt, 234 kB) für PSI-Tools
[7] WWW-Server Neuroscience der Charité (2019 nicht mehr vorhanden)
[8] Weitere Veröffentlichungen zum Nervensystem
[9] Heinz, G.: Relativität elektrischer Impulsausbreitung - Schlüssel zur Informatik biologischer Systeme (incl. Daumenexperiment) als (PDF). Siehe auch in "Bio-Modelle von Nervennetzen" (german), (english)
[10] Schoel, Gunnar; Puschmann, Peter: Neural Networks with Time Delay. (PDF) Vortrag in Bionet96. Siehe auch "Projections and Coding in Pulspropagating Networks - Virtual Experiments" p.18 (english)
Mailto: info@gheinz.de
File created Oct. 10, 1995. Nachträge von 1998. Umsortiert und ergänzt 5/2019. Stylesheets 12/2023. Literatur ergänzt 4/2024
Top http://www.gheinz.de/index.html
Mail to info@gheinz.de
Besucher seit 6. Dez. 2021:
All rights reserved, © Copyrights Gerd Heinz