How does our brain work? How can we understand nerve networks? Over the last two hundred years, scientists have discovered a lot about nerves, synapses, transmitters and details. But despite finding tens of thousands of papers on artificial neural networks (ANN) and hundrets of books about nerves, we still know nearly nothing about how nerve-networks work. So what makes nerve networks so special?
Compared to electrical networks, nerve networks are completely different. While in most electrical networks (ICs, computers) you don't have to worry much about the delay time of the connection lines, the delay times of dendrites and axons are gigantic. Later we will find, they determine the function.
The right image shows what happens when three time functions of pulses flow wave-like very slowly across a field of neurons.
Cross-interferences
form inevitably holographic structures. The "G" appears in fragments everywhere.
See also "Holomorphy and Lashley's rat experiments".
The "node abstraction" of electrical networks is therefore completely invalid for nerves. Nerve pulses are sent on delay lines: You can watch the pulse-wave as it travels, conduction speeds are typically millimeters to meters per second, while on a circuit board we talk about 30 nanoseconds per meter or 30,000 km/sec.
Electronic signal processing uses correlations for all types of signal reconstruction. Demodulation and radio reception use correlation with an oscillating circuit. Any clock input of any integrated circuit or flip-flop can be considered a correlator input. All artificial neural networks on computers ("Neural Networks (NN)" or "Artificial Neural Networks (ANN)" or "Time Delay Networks (TDN)") etc. do not work without a correlating clock.
But nerve nets do not have any clock synchronization. How could our cortex work? Can ANN model nerve nets? "Artificial Neural Nets" seem to show a different behaviour compared with the behaviour of nerve nets. 1995 I introduced the name "Interference Networks" (IN) to avoid collisions with the name "Neural Network", that stands for artifical networks. See also for an introduction some animations about IN.
Interference nets or systems have a comparable mathematical-physical background in different fields, reaching from photonic wave interference in optics over signal interference in digital filters (FIR, IIR), wave interference in Radar- or Sonar- devices to ionic pulse interference in nerve nets. Special properties are short wavelength, relative timing and non-locality of function.
If we demonstrate interference circuits with pulses - please keep in mind, that we talk about likelihoods of density modulated pulse streams. Also beware, to consider an n-dimensional nerve net in 1D or 2D as the examples may imagine!
As Karl Pribram noted, the ideas of "interference" and "holography" for nerve nets were introduced 1942 by
Karl Lashley for the interpretation of his rat experiments, see this note.
1947, at the University of Texas in Austin Lloyd A. Jeffress published a sound localization circuit. It was the auditory circuit of a barn owl, trying to interprete the horizontal localization of the ears by noise coincidence. The circuit can give an intuition for the development of acoustic photo- and cinematography.
Thinking about the pulse-like character and the slow pulse velocities on nerves we find properties, that are comparable to optical projections (images). In contrast to ANN, our IN get highest importance for projections of images through nerve nets. "Thinking" is only possible "in images or signs", not in numbers or bits. Or as C.S. Peirce (1837-1914) noted: "All thought is in signs".
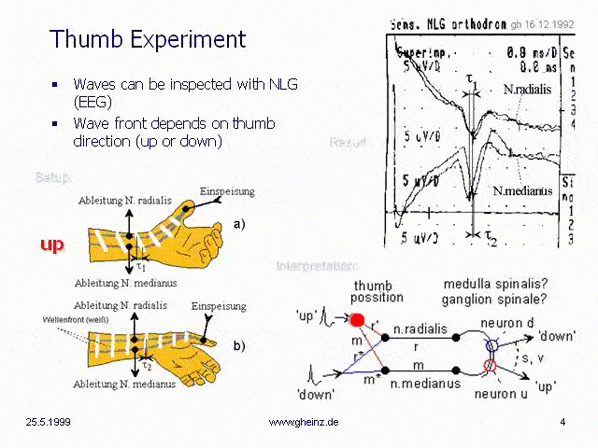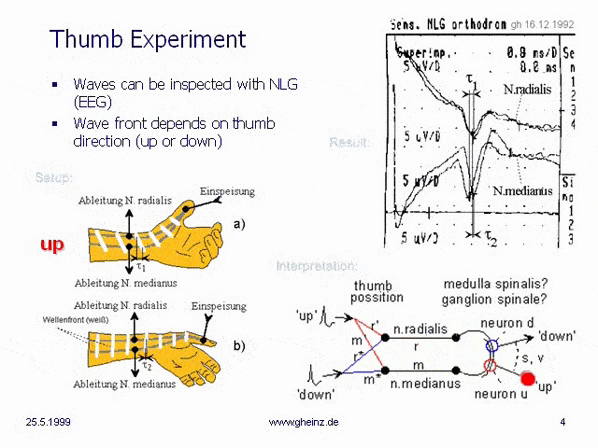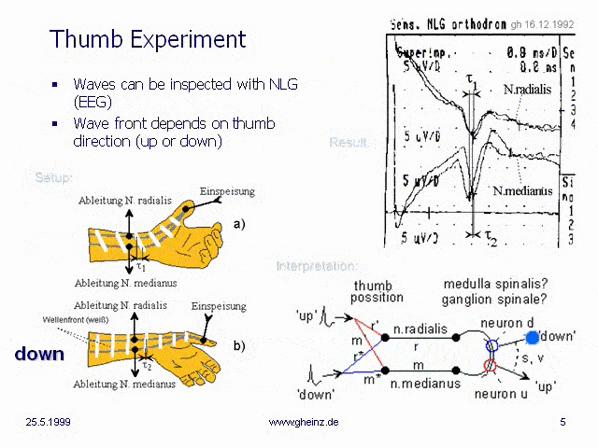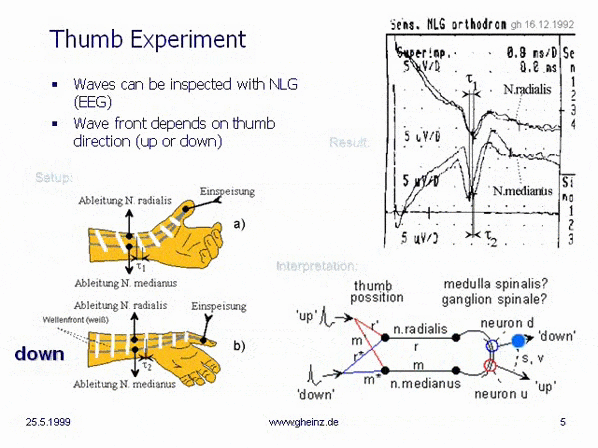
At Christmas 1992, the thumb experiment showed, that our nerve system can work as an interference system. Now the door was opened! After this successful experiment, I observed different properties of "waves on wires" in the first book about (nerve-) interference networks, written in the book "Neuronale Interferenzen" (NI93). Find a short overview about the results here.
To get interferences, we need something like "waves on wires". Can we observe such waves at any nerve net directly? Indeed, we can!
Andrew Packard found 1995
color waves on squids. He cut the spinal cord at one side. Standing color patterns changed to colored waves of excitation, see his movies.
The "Packard Glacier" in Antarctica was named for him.
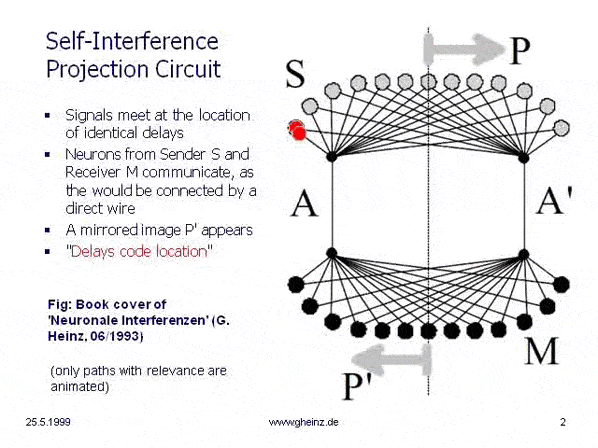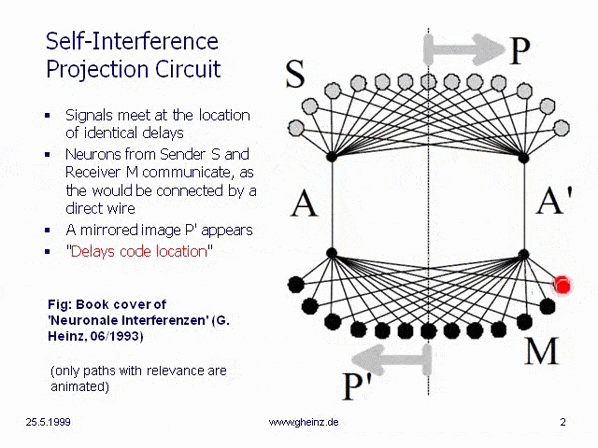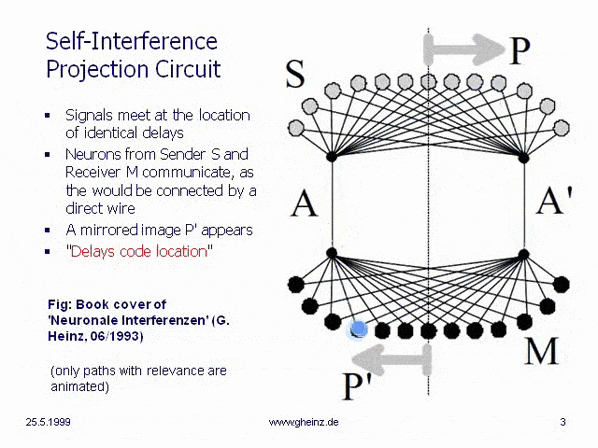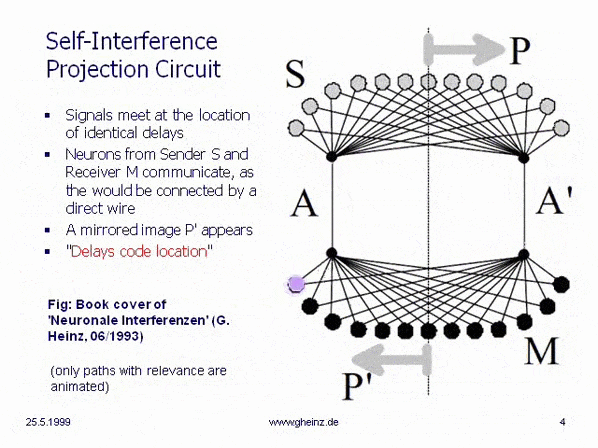
How can an interference net look like? The next circuit (source NI93) shows a simplest. (In IN the wires have limited velocities - they are not electrical nodes!) A neuron in the sending space S may fire subsequent at position P. Pulses run to and over both channels A and A' into the receiving space M and meet at P. At all other locations the pulses appear one after the other, not at the same time. The chance of exciting a neuron is highest at points of simultaneous arrival.
That receiving neuron gets the highest excitement value, where both sister pulses arrive exact at the same time. When the neuron at P fires, this is the neuron at location P'. We find: A biological interference network can transmit information only as a mirrored projection from generator space P into detector space P'.
To understand the spontaneous waves on Andrew's squids: If we cut channel A, all projections disappeare. If wire A is cut and gets a statically high level, now only the waves coming via A' run through the detector space - we see waves instead of fixed excitation locations.
So Lashleys
hologramm-idea, Jeffress
auditory circuit, Packards
waves on squids, my
thumb experiment and an
image-like,
holographic behaviour show the direction of nerve network research: We have to study wave interference circuits. That are circuits, that produce projections (like optical images) on wires without any clock synchronization.
Thus, the research followed parallel two directions: the reconstruction of nerve data (EKG, EEG, ECoG) and of sound (acoustic images & films). Following this way, in a small team together with Sabine Höfs and Carsten Busch we got in August 1994 first passive (standing) acoustic noise images applying microphones to a EEG-data recorder and using the first interference network calculator (our "Bio-Interface") for the reconstruction of acoustic data.
It was the birthplace for Acoustic Photo- and Cinematography (Acoustic Cameras), rewarded by innovation prices and producing hundrets of jobs worldwide.
A further technical background of interferences we find in the maths of Faltung (Convolution) of noise signals, usable for invisible RADAR or in the nerve system. So lets have a closer look behind the idea of interference integrals and interference patterns.
With his rat experiments, Karl Lashley found a hologram-like property of the brain. Independently which part of the brain he removed, rats could remember a before learned behaviour, published in subsequent papers since 1929. In his 1950 paper "In search of the engram" (source p.478-505) he wrote:
"It is not possible to demonstrate the isolated localization of a memory trace anywhere within the nervous system." (p.501)
As Karl Pribram noted, for fun he said once, that his rats experiments verified, that the memory of the rats is not localized within the cortex. In the same time, Denis Gabor experimented with Holography.
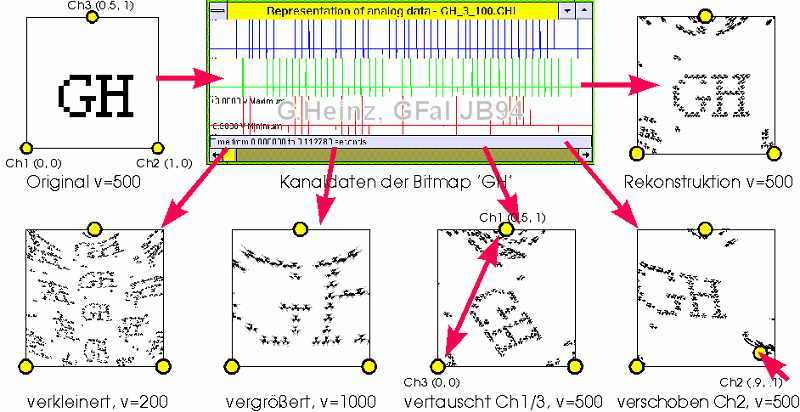Already in the GFaI-Annual Report 1994
(PDF)
the reconstruction of different time functions showed hologram-like
patterns (v=200) as an immanent property of IN, see the right image (v is the velocity).
The reason for this can be found in the pulse density. If each neuron in the generator space fires not just once, but continuously, then waves i coincide with waves i+1, i-1 etc. This creates multiple images in the detector space at different locations, see cross interferences.
The pulse spacing alone determines the distance between the images that appear many times, see the cross interference radius.
Thus hologramms appear as a law of nature by cross interferences around the location of self interference. More about cross interferences see for example here.
We had talks with Karl Pribram (1919-2015) about this topics. He sent me a part of his scheduled book 'Brain and Being' about some details:
"Lashley had proposed that interference patterns among wave fronts in brain electrical activity could serve as the substrate of perception and memory as well. This suited my earlier intuitions, but Lashley and I had discussed this alternative repeatedly, without coming up with any idea what wave fronts would look like in the brain. Nor could we figure out how, if they were there, how they could account for anything at the behavioral level. These discussions taking place between 1946 and 1948 became somewhat uncomfortable in regard to
Donald Hebb's book ("The Organization of Behavior", 1949) that he was writing at the time we were all together in the Yerkes Laboratory for Primate Biology in Florida. Lashley didn't like Hebb's formulation but could not express his reasons for this opinion: "Hebb is correct in all his details, but he's just oh so wrong."
Within a few days of my second encounter with Ernest Hilgard, Nico Spinelli a postdoctoral fellow in my laboratory, brought in a paper written by John Eccles (Scientific American, 1958) in which he stated that although we could only examine synapses one by one, presynaptic branching axons set up synaptic wavefronts. Functionally it is these wavefronts that must be taken into consideration. I immediately realized (see Fig. 1-14, Languages of the Brain 1971) that axons entering the synaptic domain from different directions would set up interference patterns.
(It was one of these occasions when one feels an utter fool. The answer to Lashly’s and my first question as to where were the waves in the brain, had been staring us in the face and we did not have the wit to see it during all those years of discussion.)"
(Karl Pribram in
'Brain and Being', 2004, Ch.12: 'Brain and Mathematics', page 217 ff. See his preview, page 4 ff)
The point of conflict was the following. Donald Hebb wrote in his book:
"When one neuron repeatedly assists in firing another, the axon of the first cell develops synaptic knobs (or enlarges them, if they already exist) in contact with the soma of the second cell".
This sentence became the guiding idea of learning algorithms in (artificial) neural network theory (NN, ANN).
But why was Hebb "correct in all his details, but oh so wrong"?
It would take 45 years to find precise answers. They are something like:
Learning is only possible, if the delay structure of the network forces interferences to the neuron, that shall be able to do something or to learn.
What is that supposed to mean? Why should delays dominate over weights? Let's look again at the cover picture of the book "Neural Interferences" from 1993 Titelbild NI93. Every pulse coming from the sending field S reaches every neuron in the receiving field M at some time.
But the more pulses reach it at the same time, the higher is the excitability of a neuron. Individual impulses are lost. This means that pulses arriving at the same time have an advantage. That is why we have to focus only on this cases. Therefore, only those cases are shown in which two impulses from above reach at the same time a neuron below.
So far so good. But what does that mean? The leftmost sending neuron can only send a message to (which can be processed by) the rightmost receiving neuron. Never it is able to send a message to a receiving neuron on the left or in the middle: the delay structure prevents this. We see: "Delays dominate over weights".
This means that not all neurons in the network can communicate with each other. In the example image, neurons that can communicate with each other are arranged in mirror image; the arrows P and P' are intended to illustrate this.
While the cables laid between the buttons and the bells establish the communication link in a doorbell system, in an interference network only the delay structure establishes the communication between sources and destinations!
So if a neuron (due to the delay structure of the network) does not have the place to receive the partial impulses from a source just at the same time, nothing can be received from this transmitter! In other words: Weight learning is impossible without the appropriate delay structure or "delays dominate over weights".
A deeper background is also, that neurons may not be excited by their direct neighbors. In order to prevent self-excitation of the entire network, delay structures also create neighborhood inhibition without doing anything.
Although he could not express it clearly, Karl Lashley had the right intuition!
For more information see "Holomorphism and Lashley's rat experiments" (Link), NI93, chap. 5, p.117 or chap. 10, p.211 or a paper from 2018, chapter 7, p.9.
Find an overview about Interference Integral Properties here english / german.
Visitors since Dec. 2021:
www.gheinz.de/historic/brainwaves.htm
Aus dem Deutschen übersetzt von https://translate.google.com mit manuellen Korrekturen