(back)
(german)

Heinz, G.: Neural Interferences.
Author equals editor. Personal distribution, 1993, 301 p.

Neural Interferences

Remarks about the Book

(Google translation with corrections)

Informations can only be linked together where they are present at the same time. Understanding this truism is obviously not easy. And yet, it holds the key to understand interference networks and the nerve system.

Digital gates in the PC or smartphone, for example, require that the signals to be linked are statically present at the inputs of a gate for a certain period of time. Computers therefore have clock-signals with clock frequencies. The time of a clock transition from high to low or vice versa defines the takeover of data into the different modules. But the clock signal has to be present on the huge integrated circuit (IC) everywhere exactly to nanoseconds at the same time.

While wires and circuits in computers transmit any signal at about a tenth the speed of light, nerve networks are around a million times slower. Also our cortex is a thousand times bigger.

Cortical signals run so slowly that they cannot be used for synchronization: the informatics of the nerve system is not that of a computer.

And as if that wasn't horror enough, nerve signals are pulse-like. We speak of "spikes". And spikes crawl extremely slowly through our brain. So how are nerve networks synchronized?

If we try to bring two spikes coming from different directions together at an AND gate (here the AND-gates A and B), pulses will never arrive at the same time at A: Because of an asymmetrical delay τ the output of gate A will remain silent, only gate B gives an answer. Digital circuits mostly don't work with spikes. Especially not when the wires are as slow as our nerves. Information can only be processed where it is present at the same time. That only leaves one conclusion: Nerve networks does't work like computers. But how do they work?

To find out how nerve-networks might work, we imagine that each nerve branches out in many directions. If we now look at spikes that are wandering around in different nerves, then we are sure to find a place where they meet each other. Only a nerve cell located at this point can be excited!

In contrast to the computer, in which logic levels (0 or 1) determine the information content, the location of the simultaneity of the meeting of different spikes determines "the information" in the nerve network. Nerve networks cannot be understood with computer informatics. They are of different nature. We are dealing with a completely different computer science.

If we think about this thought for a long time, we will discover the principle behind it: Nerve networks can only work projectively (depicting, image-like, lense like, mirroring), never static like a computer. That explains why it takes us years to learn the multiplication table. Or why memory artists have to invent a picture story in order to be able to memorize a few playing cards: We arrive at the "interference networks". The information content lays in the sharpness of a projection. Waves become images and vice versa - optics and acoustics merge under the roof of the interference networks: "Seeing is Hearing" was written on the first Acoustic Camera in 1996.

It borders on a miracle that Karl Lashley, who became famous for his rat experiments ("In search of the engram"), came to postulate interferences in nerve networks as early as 1942. Unfortunately, I only discovered the following quote in Karl Pribram's estate after his death in January 2015. Karl had sent me various articles over the years, he wrote:

"Lashley (1942) had proposed that interference patterns among wave fronts in brain electrical activity could serve as the substrate of perception and memory as well. This suited my earlier intuitions, but Lashley and I had discussed this alternative repeatedly, without coming up with any idea what wave fronts would look like in the brain. Nor could we figure out how, if they were there, how they could account for anything at the behavioral level. These discussions taking place between 1946 and 1948 became somewhat uncomfortable in regard to Don Hebb's book (1948) that he was writing at the time we were all together in the Yerkes Laboratory for Primate Biology in Florida. Lashley didn't like Hebb's formulation but could not express his reasons for this opinion: "Hebb is correct in all his details but he's just oh so wrong"."
(Karl Pribram in 'Brain and Mathematics', 1991)

Donald Hebb wrote in his book:

"When one neuron repeatedly assists in firing another, the axon of the first cell develops synaptic knobs (or enlarges them, if they already exist) in contact with the soma of the second cell".

This approach quickly became the universal, but unsuitable basis for neuro-computing (NN, ANN) for modeling neural networks worldwide.

But why said Lashley: "Hebb is correct in all his details but he's just oh so wrong"?

Because learning can only be done where the delay structure of the network ensures, that the information to be processed (pulses) arrive exactly at the same time. If a neuron does not receive the partial pulses of a source at the same time due to an unsuitable delay structure, it will neither learn nor do anything. Only a neuron whose delay structure enables code detection (chap. 10, p.210) can learn or do something. "Delays dominate over weights" I wrote different times.

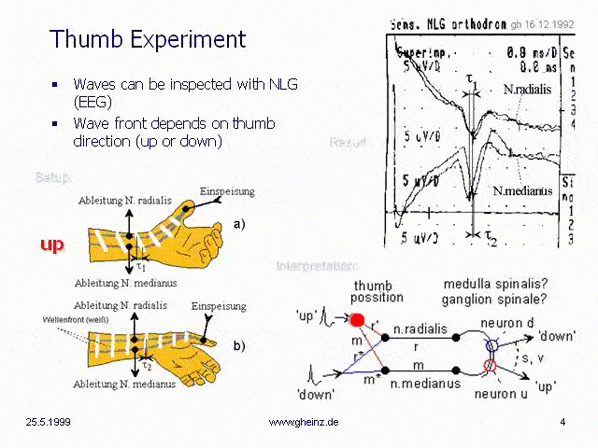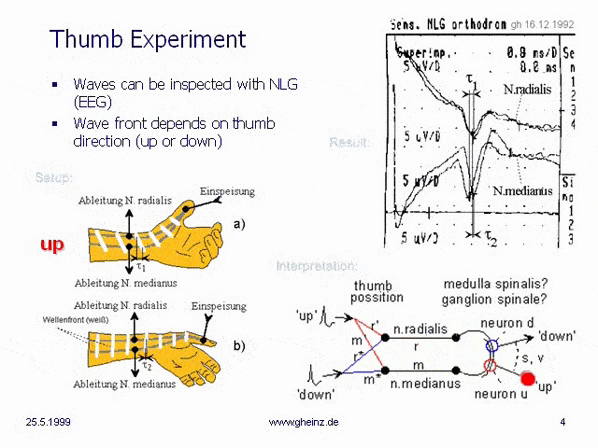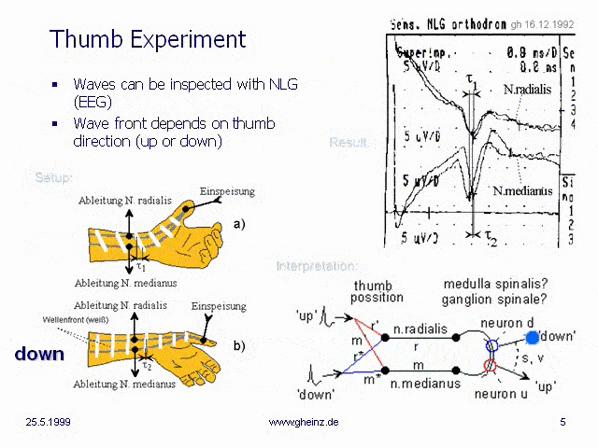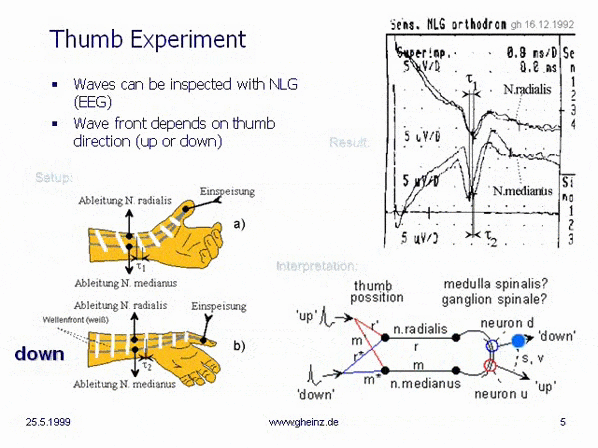With the thumb experiment in 1992, the author noticed rather accidentally, that pulses in connection with very low conduction speeds of nerves produce an unknown type of communication and information processing. The delay of needle-sharp pulses means that information can only be processed where pulses meet. Temporal patterns thus become spatial codes. Pulse waves propagate through various nerve fibers. Wherever a pulse wave interferes with itself or with another, its goal has been reached. Or where different wave fronts meet.

In order to get further in terms of ideas, a wave theory in the time domain had to be developed as well as a wave theory on discrete and inhomogeneous spaces . This is where the term 'Wave Interference Networks' came from. Ideas on the way to this unknown computer science are outlined in the manuscript.

In 1992, research on "Neural Networks" (NN, now known as Artifical Neural Nets ~ ANN) had reached a rock bottom. Faith and funding slowly dried up. Technicians increasingly rejected ANN because their learning behavior was not verifiable, whereas the biologists' approach was too mystical, see quote above. Partly catastrophic learning successes brought the end. What remained was ANN and, as a mathematical IT discipline, the so-called connectionism. The NN lacked something for the interpretation of nerve networks. But "neural networks" with clocks violate the spacetime structure of a neural network to be modeled, which leads to catastrophic modeling errors right from the start.

Digital filters use the temporal dimension, networks the spatial one. In the nerve network, however, both dimensions are linked: the greater the length, the smaller the diameter of an axon or dendrite, the greater the distance between two neurons, the greater the delay time. Extremely slow speeds together with pulse-like signals, ensure that, unlike ANN, nerve networks have to get by without a clock. How can such systems work?

Nerve networks consistently represent unsynchronized race circuits. Wherever a pulse meets its brothers, the goal is reached. That means: the delay time structure of the network alone defines the sender and recipient! Bits cannot be added on such networks. Only images or (pictorial) characters are transferable. Interference networks are bound to projections of the optical type. And these apply basically mirror-inverted.

The book also discusses n-dimensional nerve-like filters, by analogy of three-dimensional digital FIR- or IIR-filters. In order to better recognize properties, the term "interference", known from optics, seemed useful as the lowest common denominator. Information is processed where wave peaks arrive in highest, relative simultaneity. As a result, these networks were called "interference networks" (IN) by the author from 1996 onwards.

Already in 1992, the realization had matured, that pulse figures of nerve- type, if at all, can map only mirrored (see cover page). As an addressing principle in neural spaces, the thumb experiment was used to demonstrate the relativity of pulse propagation, see Chapter 6 of the thumb experiment from December 16, 1992. Unknown aspects of neural computer science far away from neural networks or Boolean algebra became apparent.

In practice, mirror-inverted images were known from optics and from nerve experiments (Penfields Homunculus, Jeffress sound location), but they could not be discovered in the literature of neurocomputing, which at that time already comprised hundreds of thousands of articles and thousands of books. In terms of system theory, something was wrong with the so-called "neural" networks. So this research began.

With the discovery of mirror-inverted pulse images, it became necessary to explore the physically real possibilities of these "delay networks" and to explore their peculiarities (zooming, movement, interference overflow, connection and decomposition, overdetermination, n-dimensionality, space-time coding, neighborhood inhibition, bursts etc.).

These investigations were successful. They led to the manuscript within four month. For example, "seeing" and "hearing" merge through investigations into self-interference (vision maps) and cross-interference (hearing maps). This knowledge formed the basis for the development of the first acoustic images and films between 1995 and 1996 and acoustic imaging par excellence for first Acoustic Cameras.

Actually only intended as a reminder, it was necessary to sketch in the shortest possible time the approximate direction of a paradigm shift from a mathematical to a physical, wave-theoretical view on nerve networks (pulse waves on ionic channels).

Interference networks (IN) can be discovered in a variety of tasks, from optics to digital race-circuits, radar, sonar, GPS, beamforming, neural networks and signal processing. From this point of view, digital circuits, state machines, digital filters, pattern or weight networks (ANN) represent IN-subgroups with discrete timing. Nerve networks are only used as a synonym for sketching a vision of a more abstract system theory, that of interference networks. The diversity of the areas of knowledge concerned literally pushed for a theoretical basis of a more abstract nature. Like digital filters, Boolean algebras are only a sub-area of interference networks.

There are some names in the book that must be considered inappropriate today. For example, Teuvo Kohonen ** questioned the use of the term "convolution" in 1995 (e.g. "Faltung", KA06.pdf, page 147). Here we come across a peculiarity of interference systems, which may be the reason for the hurdle-rich access.

While the multiplicative, one-dimensional interference of two impulses on an electrical wire has the analogy of the mathematical convolution (here we can fold the time axis), we do not use the term in two-dimensional or higher-dimensional space the convolution completely, since no convolution of the time axis can be carried out here. For this purpose, the "mask algorithm" was introduced, which also includes the one-dimensional convolution integral as an interference integral. More, modeling the sciatic nerve experiment with wave deletion, Chapter 6, p.144, convolution- and interference-integrals refuse too.

A demarcation between the interference integral and the convolution integral was presented in 2011 in Bangkok. A Javascript calculation table was designed on the subject of convolution integral versus interference integral, which tries to make things clearer. There it is shown, that the convolution integral and the interference integral (in one-dimensional space) are identical. We owe a proof approach to Alfred Fettweis, who derived the identity of the interference integral and the convolution integral for the one-dimensional case (see there).

If we take time functions between the generating space and the detecting space as so-called channel data, the question of the predictability of the images in both spaces arises. If we want to calculate the generator space, we speak of (non-reversed) reconstruction, if the detector space is to be calculated, of (mirror-inverted) projection. Both differ only in the direction of the time axis or in the direction of the delays. PSI-Tools or NoiseImage only calculate the reconstruction integral, in order to calculate the projection, the time axis could be inverted with PSI-Tools (function removed in NoiseImage).

The approach for projection and reconstruction (as a basis, for example for acoustic photo and cinematography) was laid with this book, see mask algorithm, Chapter 14, p.284. For more information, see mirrored interference projections of type f(t-T) , or right-sided interference reconstruction of type f(t+T) .

Since publications of algorithmic nature have been against the commercial usability of the results since first acoustic images appeared, these were only sparse.

In brief, a key statement of the manuscript reads as follows: Nerve networks can only be adequately simulated with a three-dimensional, electrical network simulation. Each network node requires spatial coordinates. Each branch needs his special delay. All delays that can be read from the three-dimensional structure of the nerve network must be mapped very precisely: These essentially form the function ("form codes behavior"). In addition, static (stimulating or inhibiting) synapses and threshold value parameters must of course be observed. Wave-deletion on bidirectional branches needs to be modelled.

The first application of the book for acoustic imaging showed success just two years later (1995): the world's first acoustic images and films were created with the software "Bio-Interface" later called "PSI-Tools" (Parallel and Serial Interference Tools, Sabine Höfs & Gerd Heinz).

The book manuscript including all formulas and images was created using Lotus Ami Pro written under Windows3.1. Ami Pro was arguably the most efficient and best word processor ever.

Formula editor, drawing program and tables worked within the text program, it was not only the first WYSIWYG (What You See Is What You Get) program, books could also be written with it. Paragraph formats were defined (for title, text, image, formula, etc.) and saved in a *.sty file (style sheet). This file was accessed from all chapters in the book.

Unfortunately the justification only worked correctly up to Windows98. Corrections could therefore only be incorporated until about the turn of the millennium. The date on the cover was probably set to 'File Creation Date'.

The manuscript was created with own resources. It had to be ended in May 1993, as a job with the employer GFaI e.V. was due from June 1, 1993. Without Ami Pro it would not have been possible to write this book in such a short time. Smaller additions and corrections followed until the beginning of 1994 (e.g. the section on the barn owl had been added in Chapter 1 "Jeffress delay model 1948"). 1993, Mark Konishi published the thoughts of his teacher Jeffres on hearing location parallel to the NI manuscript ***.

The original chapter 10 (Interference Logic) failed in the beginning. Mathematical modeling was attempted here, which turned out to be too narrow. After simulative verifications with Peter Puschmann and Gunnar Schoel (FHTW 1994), the Chapter was later exchanged for the Chapter "Elementary Functions of the Neuron", see also the original table of contents from 1993 (there are also old references in the index).

The book was actually written as a working manuscript. Connections and ideas should not only be noted on a sketch pad. Including all the pictures and formulas written in one hundred days (January 1993 to May 1993), the details are partially immature, the formulations are still uncertain, and every now and then it is euphoric without the reader always being able to understand it. It clearly shows the turmoil in which a new field of knowledge is unfolding. In short: one misses the rounding of mature works. Nevertheless, it still seems worth reading today. Many general findings are still brand new.

To speak with Thomas S. Kuhn*: In retrospect, the manuscript shows the obstacles on the way, but not the brilliance of the abstractions. It is more suitable for science historians than for students. Nevertheless: It is the book to which we owe acoustic imaging and to which we could gradually owe a consolidation of neuroscience: If only these basics were teached.

Today, thirty years later (2023), it is still not known that any university in the world would give a course on "Interference Networks".

The problem: biologists and physicians only have rudimentary physics, computer science and mathematics education; physicists don't know about biology or neuro-anatomy. This is extremely sad because an understanding of the nerve system is only possible when the neuroscientist has mastered these fundamentals all together. New research remains fragmentary as long as interference networks are not understood. You can't forge steel without knowledge about the fire. That should encourage sponsors be aware.

Since no real book has yet been written (it would be too early for that), but I keep receiving requests for explanatory materials on interference networks, this working manuscript will remain on the web as long as nothing better is available.

Sometimes the journey is the goal.

* Kuhn, Thomas Samuel: The Structure of Scientific Revolutions. Uni Chicago Press, 1962
** Kohonen, Teuvo: http://www.cis.hut.fi/research/som-research/teuvo.html
*** Konishi, Mark: The sound localization of the barn owl. Spectrum of Science, June 1993, pp.58-71